Theorem (Cauchy-Maclaurin Integral Test)
Let $f(x)$ be a continuous, positive, decreasing function on $[1,\infty)$ in which $f(n)=a_n$. Then $\sum_{n=1}^\infty a_n$ converges if $\int_1^\infty f(x)dx$ is finite and diverges if the integral is infinite.
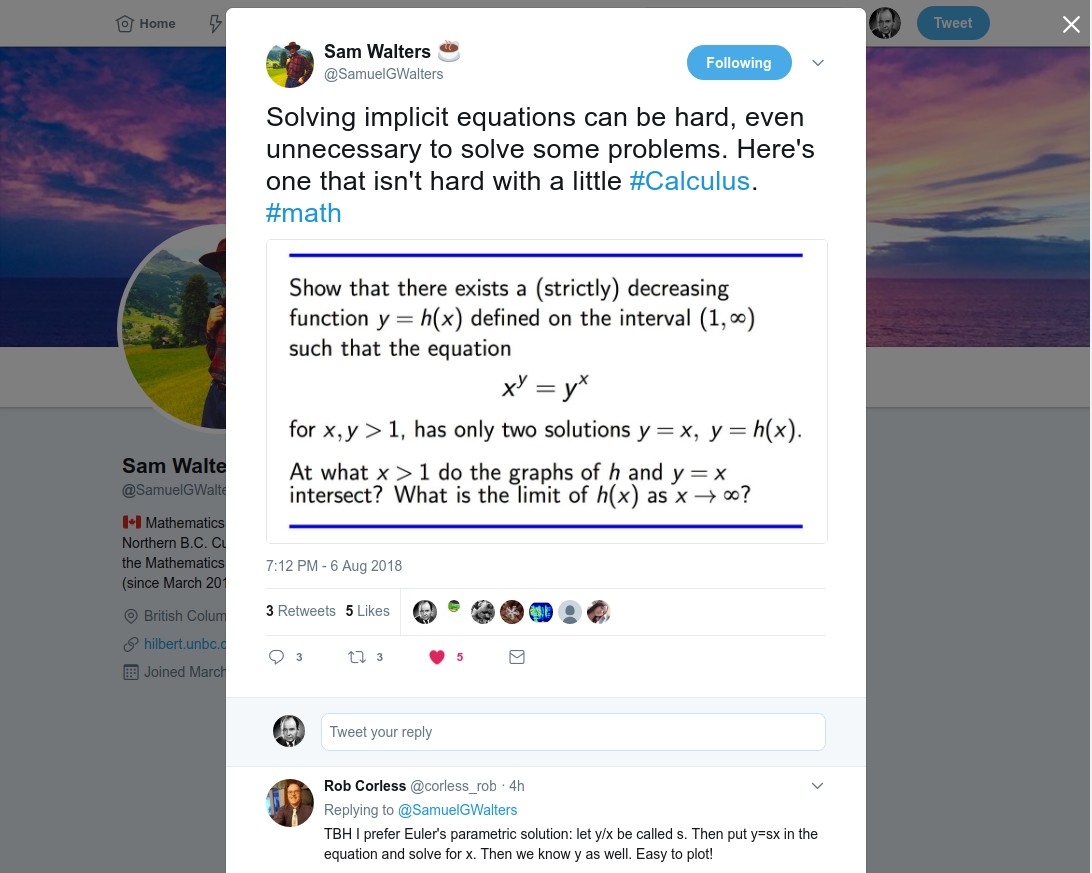
Proof. Using the left-end point method as seen in Figure 1
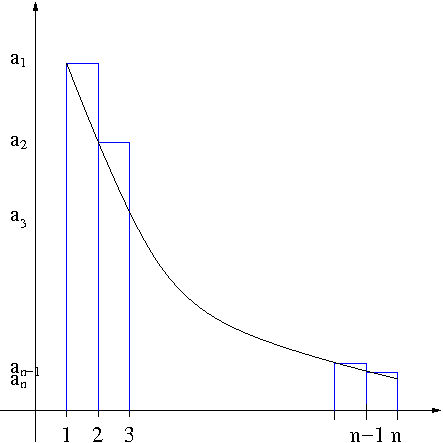
Figure 1. Integral Test
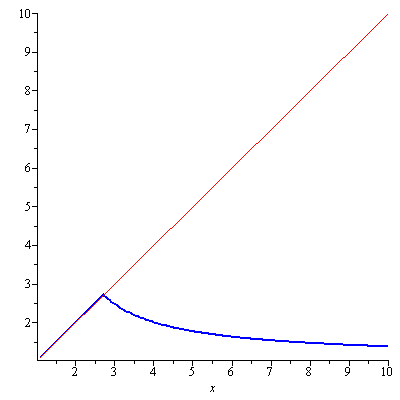
we see that $$a_1+a_2+\cdots+a_{n-1}\geq \int_1^nf(x)dx$$ This means that if $\int_1^{\infty}f(x)dx$ is infinite, $\sum_{n=1}^\infty a_n$ diverges. Now using the right-end point method as seen in Figure 2
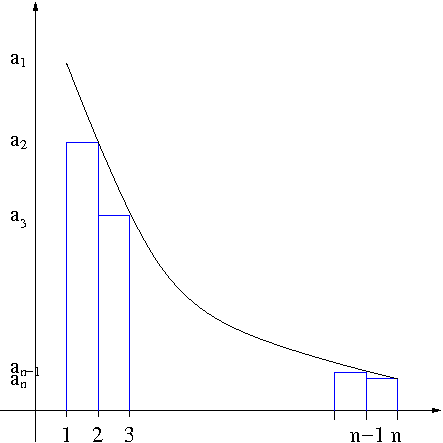
Figure 2. Integral Test
we see that $$a_2+a_3+\cdots+a_n\leq\int_1^n f(x)dx$$ This means that if $\int_1^\infty f(x)dx$ is finite, then $\sum_{n=1}^\infty a_n$ converges. This completes the proof.
Example (The $p$-series).
For what values of $p$ is the series $\sum_{n=1}^\infty\frac{1}{n^p}$ convergent?
Solution. If $p<0$ then $\lim_{n\to\infty}\frac{1}{n^p}=\infty$. If $p=0$ then $\lim_{n\to\infty}\frac{1}{n^p}=1$. In either case, $\lim_{n\to\infty}\frac{1}{n^p}\ne 0$, so the series diverges. If $p>0$ then the function $f(x)=\frac{1}{x^p}$ is continuous, positive and decreasing on $[1,\infty)$.
Now,
$$\int_1^\infty\frac{1}{x^p}dx=\left\{\begin{array}{ccc}
\left.\frac{x^{-p+1}}{-p+1}\right|_1^\infty & {\rm if} & p\ne 1,\\
\\
\ln x|_1^\infty & {\rm if} & p=1.
\end{array}\right.$$
Therefore the series converges if $p>1$ and diverges if $p\leq 1$.
Example. Test the series $\sum_{n=1}^\infty\frac{1}{n^2+1}$ for convergence or divergence.
Solution. $f(x)=\frac{1}{x^2+1}$ is continuous, positive and decreasing on $[1,\infty)$. \begin{align*}\int_1^\infty\frac{1}{x^2+1}dx&=\left.\arctan x\right|_1^\infty\\&=\arctan \infty-\arctan 1\\&=\frac{\pi}{4}\end{align*} Therefore, by the Integral Test the series converges.
Example. Determine whether $\sum_{n=1}^\infty\frac{\ln n}{n}$ converges or diverges.
Solution. $f(x)=\frac{\ln x}{x}$ is continuous, positive and decreasing on $[3,\infty)$. (One can easily check $f(x)$ is decreasing on $(e,\infty)$ by its derivative $f'(x)$.) \begin{align*}\int_3^\infty\frac{\ln x}{x}dx&=\frac{1}{2}\left.(\ln x)^2\right|_3^\infty\\&=\infty\end{align*} Therefore, $\sum_{n=1}^\infty \frac{\ln n}{n}$ diverges.
Example. Use the integral test to show that the series $$\sum_{n=1}^\infty\frac{1}{a^{\ln x}}$$ converges if $a>e$ and diverges if $0<a\leq e$.
Proof. Let $f(x)=\frac{1}{a^{\ln x}}$. Then $f(x)$ is positive and continuous on $(1,\infty)$. If $0<a<1$ then the series $\sum_{n=1}^\infty\frac{1}{a^{\ln n}}$ diverges because the sequence $\left\{\frac{1}{a^{\ln n}}\right\}$ is increasing. If $a=e$, the series becomes the harmonic series $\sum_{n=1}^\infty\frac{1}{n}$ which diverges. Now we assume that $1\leq a< e$ or $a>e$. Then $f(x)$ is decreasing $(1,\infty)$. \begin{align*}\int_1^\infty\frac{dx}{a^{\ln x}}&=\int_1^\infty a^{-\ln x}dx\\&=-\int_0^{-\infty}a^ue^{-u}du\ (u=-\ln x,\ dx=-xdu=-e^{-u}dx)\\&=\int_{-\infty}^0a^ue^{-u}du\end{align*} Let $v=a^u$ and $dw=e^{-u}du$. Then $dv=a^u\ln a du$ and $w=-e^{-u}$. The integration by parts formula $\int vdw=vw-\int wdv$ results in $$\int a^ue^{-u}du=-a^ue^{-u}+\ln a\int e^{-u}a^udu+C’$$ Hence we find $$\int a^ue^{-u}du=\frac{a^ue^{-u}}{\ln a-1}+C$$ \begin{align*}\int_1^\infty\frac{dx}{a^{\ln x}}&=\int_{-\infty}^0a^ue^{-u}du\\&=\left[\frac{a^ue^{-u}}{\ln a-1}\right]_{-\infty}^0\\&=\frac{1}{\ln a-1}\left\{1-\lim_{u\to -\infty}\frac{a^u}{e^u}\right\}\end{align*} While $\frac{a^u}{e^u}$ is an indeterminate form of type $\frac{\infty}{\infty}$, the L’Hôpital’s Rule is not helpful for finding the limit $\lim_{u\to -\infty}\frac{a^u}{e^u}$ as $\frac{(a^u)’}{(e^u)’}=\frac{a^u\ln a}{e^u}$. Instead let $y=\frac{a^u}{e^u}$. Then $\ln y=u(\ln a-1)$. $$\lim_{u\to -\infty}\ln y=\left\{\begin{array}{ccc}-\infty & \mbox{if} & a>e\\\infty & \mbox{if} & a<e\end{array}\right.$$ i.e. $$\lim_{u\to -\infty}\frac{a^u}{e^u}=\left\{\begin{array}{ccc}e^{-\infty}=0 & \mbox{if} & a>e\\e^{\infty}=\infty & \mbox{if} & a<e\end{array}\right.$$ Therefore, $$\int_1^\infty\frac{dx}{a^{\ln x}}=\left\{\begin{array}{ccc}\frac{1}{\ln a-1}<\infty & \mbox{if} & a>e\\\infty & \mbox{if} & a<e\end{array}\right.$$ This completes the proof.
Theorem (Remainder Estimate for the Integral Test)
If $\sum_{n=1}^\infty a_n$ converges by the Integral Test and $R_n=S-s_n$, then
\begin{equation}\label{eq:remest}\int_{n+1}^\infty f(x)dx\leq R_n\leq\int_n^\infty f(x)dx\end{equation}
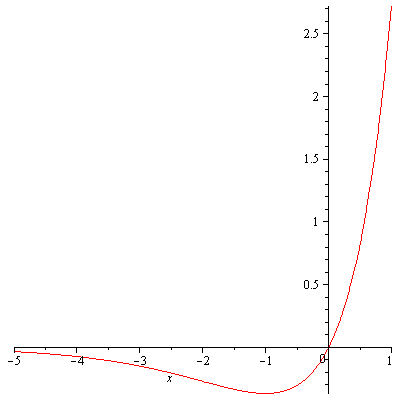
Proof. Using the left-end point method we obtain $$R_n=a_{n+1}+a_{n+2}+\cdots\geq\int_{n+1}^\infty f(x)dx$$ as seen in Figure 3.
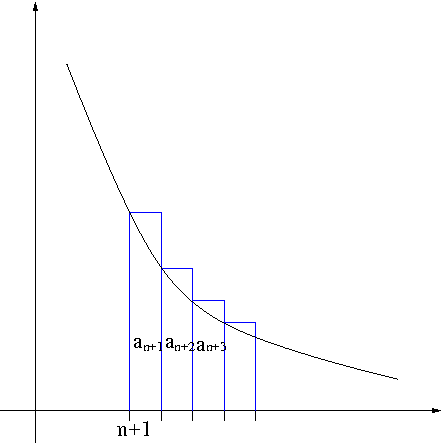
Figure 3. Remainder Estimate
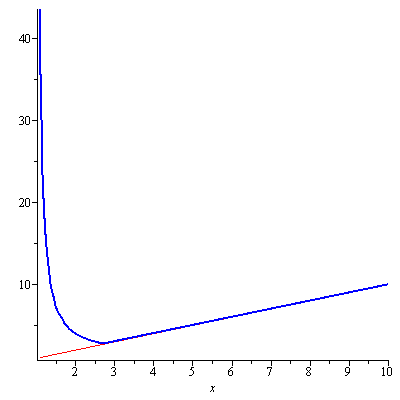
Now using the right-end point method we obtain $$R_n=a_{n+1}+a_{n+2}+\cdots\leq\int_n^\infty f(x)dx$$ as seen in Figure 4.
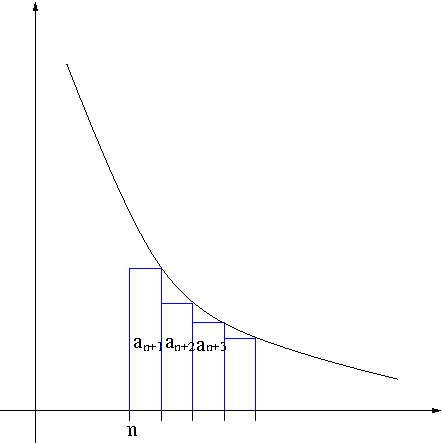
Figure 4. Remainder Estimate
Hence proves \eqref{eq:remest}.
Example.
- Approximate the sum of the series $\sum_{n=1}^\infty\frac{1}{n^3}$ by using the sum of the first 10 terms. Estimate the error involved in this approximation.
- How many terms are required to ensure that the sum is accurate to within $0.0005$?
Solution. First we calculate $$\int_n^\infty\frac{1}{x^3}dx=\frac{1}{2n^2}$$
- $s_{10}=\frac{1}{1^3}+\frac{1}{2^3}+\cdots+\frac{1}{10^3}\approx 1.197532$. By the remainder estimate \eqref{eq:remest} $$R_{10}\leq\int_{10}^\infty\frac{1}{x^3}dx=\frac{1}{200}=0.005$$ So the size of the error is at most 0.005.
- $R_n\leq\int_n^\infty\frac{1}{x^3}dx=\frac{1}{2n^2}$. Suppose $\frac{1}{2n^2}<0.0005$. Then we find $n>\sqrt{1000}\approx 31.6$. This means we need 32 terms to guarantee accuracy to within 0.0005.
Corollary. \begin{equation}\label{eq:sumest}s_n+\int_{n+1}^\infty f(x)dx\leq s\leq s_n+\int_n^\infty f(x)dx\end{equation}
Proof. Add $s_n$ to each side of the inequalities in \eqref{eq:remest}
Example. Use the inequality \eqref{eq:sumest} with $n=10$ to estimate the sum of the series $\sum_{n=1}^\infty\frac{1}{n^3}$.
Solution. Using \eqref{eq:sumest} for $n=10$ we have $$s_{10}+\int_{11}^\infty\frac{1}{x^3}dx\leq s\leq s_{10}+\int_{10}^\infty\frac{1}{x^3}dx$$ i.e. $$s_{10}+\frac{1}{2(11)^2}\leq s\leq s_{10}+\frac{1}{2(10)^2}$$ Hence we get $$1.201664\leq s\leq 1.202532$$ We can approximate $s$ by taking the midpoint of this interval (i.e. the average of the boundary points) which is $s\approx 1.2021$. The error is then at most half the length of the interval i.e. the error is smaller than 0.0005. Recall that we had to use 32 terms to make error smaller than 0.0005 in the previous example but in this example we needed only 10 terms. So we can obtain a much improved estimate using \eqref{eq:sumest} than using $s_n$.