There is a close relatioship between continuity and differentiability, namely

Theorem 18. If $f'(x_0)$ exists then $f(x)$ is continuous at $x_0$; i.e. $\displaystyle\lim_{x\to x_0}f(x)=f(x_0)$. However the converse need not be true.

Proof. \begin{eqnarray*}\lim_{x\to x_0}[f(x)-f(x_0)]&=&\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\cdot(x-x_0)\\&=&f'(x)\cdot 0\\&=&0.\end{eqnarray*}

Example. [A Counterexample for the Converse] The function $f(x)=|x|$ is continuous at $x=0$ but has no derivative at $x=0$.

Proof. \begin{eqnarray*}\lim_{x\to 0+}\frac{f(x)-f(0)}{x-0}&=&\lim_{x\to 0+}\frac{|x|}{x}\\&=&\lim_{x\to 0+}\frac{x}{x}\\&=&1,\end{eqnarray*} while \begin{eqnarray*}\lim_{x\to 0-}\frac{f(x)-f(0)}{x-0}&=&\lim_{x\to 0-}\frac{|x|}{x}\\&=&\lim_{x\to 0-}\frac{-x}{x}\\&=&-1.\end{eqnarray*} Hence, $f'(0)=\displaystyle\lim_{x\to 0}\frac{f(x)-f(0)}{x-0}$ does not exist.

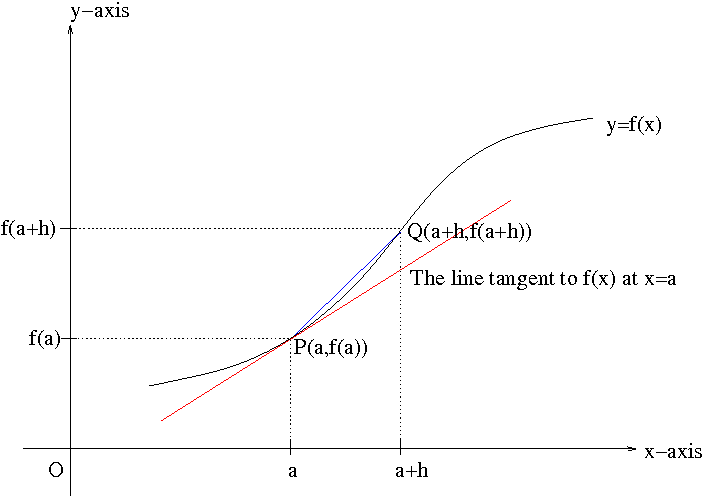
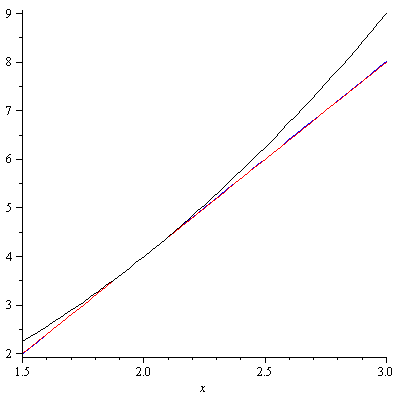
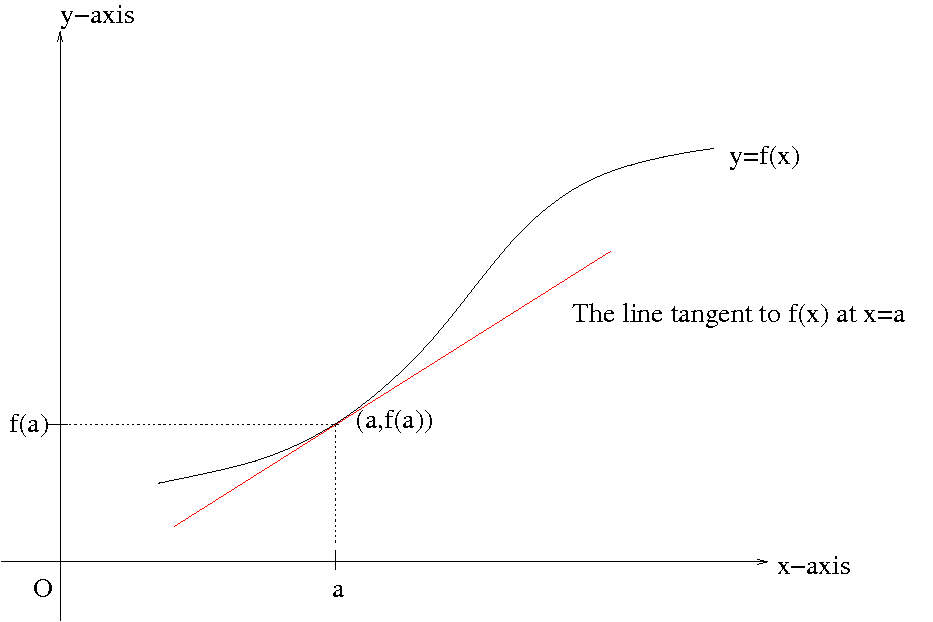Let us recall the definition of the derivative $$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}.$$ Replace $h$ by $\Delta x$. Then $f'(x)$ is rewritten as $$f'(x)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}.$$ In mathematics, $\Delta$ often means an increment. So $\Delta x$ means an increment of $x$. Note that $\Delta x$ could be positive or negative. Denote by $\Delta y$ the difference $f(x+\Delta x)-f(x)$. $\Delta y$ is called an increment of $y$. Hence, the average rate of change of $y$ with respect to $x$ in the interval $[x,x+\Delta x]$ is the difference quotient $$\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}.$$  In the view of Gottfried Leibniz, one could think of $\Delta x$ as becoming infinitesimal. The resulting quantity is denoted by $dx$. When $\Delta x$ becomes the infinitesimal $dx$, $\Delta y$ simultaneously becomes the infinitesimal $dy$. The infinitesimals $dx$ and $dy$ are called differentials. Hence the ratio $\frac{\Delta y}{\Delta x}$ becomes $\frac{dy}{dx}$ accordingly, and it is exactly equal to $f'(x)$. The quantity $\frac{dy}{dx}$ can be viewed as the ratio of differentials or as s synonym for $f'(x)$.

Leibniz Notation: If $y=f(x)$, the derivative $f'(x)$ can be written $$\frac{dy}{dx},\frac{df(x)}{dx},\ \mbox{or}\ \frac{d}{dx}f(x).$$ This is just a notation and does not represent a division. Using Leibniz notaion, the value $f'(a)$ of $f'(x)$ at a specific point $x=a$ can be written $$\left.\frac{dy}{dx}\right|_{x=a}\ \mbox{or}\ \left.\frac{df(x)}{dx}\right|_{x=a}.$$

Calculating derivatives using the limit defintion can be really laborious. In actual practice, special rules and formulas are derived for differentiating certain types of functions. The following are such rules and they can be proved striaghtforwardly by the definition of the derivative.

Theorem 15. Let $c$ be a constant, and $f(x)$ and $g(x)$ be two differentiable functions of $x$.

1. $\displaystyle\frac{dc}{dx}=0$
2. $\displaystyle\frac{d(cf(x))}{dx}=c\frac{df(x)}{dx}$
3. $\displaystyle\frac{d[f(x)+g(x)]}{dx}=\frac{df(x)}{dx}+\frac{dg(x)}{dx}$

The converse of the first rule is also true, namely if $f'(x)=0$ for all $x$ in the domain then $f(x)$ is a constant function. This will be proved later.

Lemma 16. [Binomial Theorem] \begin{eqnarray*}(a+b)^n&=&\begin{pmatrix}n\\0\end{pmatrix}a^nb^0+ \begin{pmatrix}n\\1\end{pmatrix}a^{n-1}b+\begin{pmatrix}n\\2\end{pmatrix}a^{n-2}b^2+\cdots+\begin{pmatrix}n\\k\end{pmatrix}a^{n-k}b^k+\\&&\cdots+\begin{pmatrix}n\\n-1\end{pmatrix}ab^{n-1}+\begin{pmatrix}n\\n\end{pmatrix}a^0b^n\\&=&a^n+\begin{pmatrix}n\\1\end{pmatrix}a^{n-1}b+\begin{pmatrix}n\\2\end{pmatrix}a^{n-2}b^2+\cdots+\begin{pmatrix}n\\k\end{pmatrix}a^{n-k}b^k+\\&&\cdots+\begin{pmatrix}n\\n-1\end{pmatrix}ab^{n-1}+b^n,\end{eqnarray*} where $$\begin{pmatrix}n\\k\end{pmatrix}=\frac{n!}{k!(n-k)!}.$$ $\begin{pmatrix}n\\k\end{pmatrix}$ is also denoted by $n{\mathrm C}k$. The binomial coefficients $\begin{pmatrix}n\\k\end{pmatrix}$ can be also easily obtained by Pascal’s triangle. For details see here and here.

Theorem 17. [Power Rule] $\displaystyle\frac{dx^n}{dx}=nx^{n-1}$

Proof. Let $y=x^n$. Then by the Binomial Theorem \begin{eqnarray*}\frac{dx^n}{dx}&=&\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}\\&=&\lim_{\Delta x\to 0}\frac{(x+\Delta x)^n-x^n}{\Delta x}\\&=&\lim_{\Delta x\to 0}\frac{\left[x^n+nx^{n-1}\Delta x+\frac{n(n-1)}{2!}x^{n-2}(\Delta x)^2+\cdots+(\Delta x)^n\right]-x^n}{\Delta x}\\&=&\lim_{\Delta x\to 0}\left[nx^{n-1}+\frac{n(n-1)}{2!}x^{n-2}\Delta x+\cdots+(\Delta x)^{n-1}\right]\\&=&nx^{n-1}.\end{eqnarray*}

Example. If $y=3x^5$, then by Property 2 of Theorem 15 and Power Rule (Theorem 17), we have \begin{eqnarray*}\frac{dy}{dx}&=&3\frac{dx^5}{dx}\\&=&3(5)x^{5-1}\\&=&15x^4.\end{eqnarray*}

Remark. In Theorem 17 Power Rule is established only for the case when $n$ is a positive integer. The formula is indeed valid for all real $n$’s.

Example. If $y=8x^{-\frac{3}{4}}$, then we have $$\frac{dy}{dx}=8\left(-\frac{3}{4}\right)x^{-\frac{3}{4}-1}=-6x^{-\frac{7}{4}}.$$

Using Theorems 15 and 17, we can now find the derivative of any polynomial function.

Example. If $y=2x^4-x^3-2x+7$, then \begin{eqnarray*}\frac{dy}{dx}&=&\frac{d(2x^4)}{dx}-\frac{d(x^3)}{dx}-2\frac{dx}{dx}+\frac{d(7)}{dx}\\&=&8x^3-3x^2-2.\end{eqnarray*}

Example. The function $f(x)=\displaystyle\frac{3x^3-4}{x^2}$ does not appear to be a power function, but it actually can be written as a power function. $$f(x)=\frac{3x^3-4}{x^2}=\frac{3x^3}{x^2}-\frac{4}{x^2}=3x-4x^{-2}.$$ Hence we have $$f'(x)=\frac{d(3x)}{dx}-\frac{d(4x^{-2})}{dx}=3+8x^{-3}.$$

Example. The function $y=\root 3\of{x^2}-3\root 3\of{x}-5$ can be also written as a power function. \begin{eqnarray*}y&=&\root 3\of{x^2}-3\root 3\of{x}-5\\&=&(x^2)^{\frac{1}{3}}-3x^{\frac{1}{3}}-5\\&=&x^{\frac{2}{3}}-3x^{\frac{1}{3}}-5.\end{eqnarray*} Hence, $$\frac{dy}{dx}=\frac{2}{3}x^{-\frac{1}{3}}-x^{-\frac{2}{3}}.$$

Let us assume that a particle is moving along a straight line and that the function $s=f(t)$ describes the position of moving particle at the time $t$. In physics, such a function $s=f(t)$ is called a motion.

Suppose the particle passes the points $P$ and $Q$ at the times $t$ and $t+\Delta t$, respectively. If $s$ and $s+\Delta s$ are the respective distances from some fixed point $O$, then the average velocity of the particle during the time interval $\Delta t$ is $$\frac{\Delta s}{\Delta t}=\frac{f(t+\Delta t)-f(t)}{\Delta t}=\frac{\mbox{Distance Traveled}}{\mbox{Time Elapsed}}.$$ The instantaneous velocity $v$ of the particle at the time $t$ is then given by the derivative of motion $s=f(t)$ $$v=\frac{ds}{dt}=\lim_{\Delta t\to 0}\frac{\Delta s}{\Delta t}.$$ In physics, the intantaneous velocity is also denoted by $\dot{s}$ or $\dot{f}(t)$. This dot notation was introduced by Sir Issac Newton.

Similaryl, if $\Delta v$ is the change in the velocity of the particle as it moves from $P$ to $Q$ during the time interval $\Delta t$, then $$a=\frac{dv}{dt}=\lim_{\Delta t\to 0}\frac{\Delta v}{\Delta t}$$ is the acceleration of the particle at the time $t$. Using dot notation, the acceleration is also denoted by $\dot{v}$, $\ddot{s}$, $\ddot{f}(t)$, or $\frac{d^2 s}{dt^2}$. The last notation $\frac{d^2 s}{dt^2}$ is due to Gottfried Leibniz.

If a body is thrown vertically upward with a certain initial velocity $v_0$, its distance $s$ from the starting point is given by the formula $$s(t)=v_0t-\frac{1}{2}gt^2,$$ where $g$ is the gravitational constant $g=9.8\mbox{m}/\mbox{sec}^2=32\mbox{ft}/\mbox{sec}^2.$

Example. From the top of a building 96 feet high, a ball is thrown directly upward with a velocity of 80 feet per second. Find (a) the time required to reach the highest point, (b) the maximum height attained, and (c) the velocity of the ball when it reaches the ground.

Solution. $v_0=80$ ft/sec and $g=32\mbox{ft}/\mbox{sec}^2$, so $$s=80t-16t^2$$ and $$v=\frac{ds}{dt}=80-32t.$$

(a) At the heighest point, $v=0$ that is $0=80-32t$. So, $t=\frac{5}{2}$.

(b) $s\left(\frac{5}{2}\right)=80\left(\frac{5}{2}\right)-16\left(\frac{5}{2}\right)^2=100$ft. Hence the height of the ball above the ground is 196 feet.

(c) Since the ball will reach the ground when $s=-96$, it follows that $-96=80t-16t^2$ or $16(t-6)(t+1)=0$. Hence $t=6$ and the velocity is $v(6)=80-32\cdot 6=-112$ft/sec when the ball strikes the ground. The negative sign merely indicates that the velocity of the ball is directed downward.

In this lecture, I am going to introduce you a new idea, which was discovered by Sir Issac Newton and Gottfried Leibiz, to find the slope of a tangent line. This is in fact a quite ingenious idea as you will see. Let a function $y=f(x)$ be given. We want to find the slope of a line tangent to the graph of $y=f(x)$ at a point $x=a$. First consider another point on the $x$-axis that is away from $x=a$. If the distance from $x=a$ to this point is $h$, then the point can be written as $x=a+h$. Let $P(a,f(a))$ and $Q(a+h,f(a+h))$. Then the slope of line segment $\overline{PQ}$ is given by $$\frac{f(a+h)-f(a)}{h}.$$

Now we continuously change $h$ so that it gets smaller and smaller close to $0$, consequently the point $a+h$ gets closer to $a$. We want to see how the rate $\frac{f(a+h)-f(a)}{h}$ changes as $h\to 0$. To illustrate the situation better, I will use a specific example, say $f(x)=x^2$ with $a=2$. First we take $h=1$. The following picture shows you the graph of $f(x)=x^2$ (in black), where $1.5\leq x\leq 3$ and the line through $P(2,4)$ and $Q(2+h,(2+h)^2)$ (in blue), and the line tangent to the graph $f(x)=x^2$ at $x=2$ (in red).

Next we take $h=0.5$. Then the picture becomes

For $h=0.1$, the picture becomes

As one can clearly see, the line through $P(2,4)$ and $Q(2+h,(2+h)^2)$ gets closer to the tangent line as $h$ gets smaller close to $0$. We can still do better. For $h=0.001$, the picture becomes

The line through $P(2,4)$ and $Q(2+h,(2+h)^2)$ and the tangent line now appear to be overlapping. From this observation, we can see that the rate $\frac{f(a+h)-f(a)}{h}$ gets closer and closer to the slope of tangent line as $h$ gets smaller and smaller close to $0$. In fact, the slope would be exactly the limit of $\frac{f(a+h)-f(a)}{h}$ as $h$ approaches $0$. Denote the limit by $f'(a)$. Then $$f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}.$$ $f'(a)$ is called the derivative of $f(x)$ at $x=a$. One may wonder why we need another name for the slope of a tangent line. The reason is that as we will see later the slope of a tangent line can mean something else in different contexts. Let $x=a+h$. Then $x\to a$ as $h\to 0$. So $f'(a)$ can be also written as $$f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}.$$ The equation of tangent line to $y=f(x)$ at $x=a$ is then given by $$y-f(a)=f'(a)(x-a).$$

Example. Find the equation of tangent line to the graph of $f(x)=x^2$ at $x=2$.

Solution. First we need to find $f'(2)$, i.e. the slop of the tangent line. \begin{eqnarray*}f'(2)&=&\lim_{h\to 0}\frac{f(2+h)-f(2)}{h}\\&=&\lim_{h\to 0}\frac{(2+h)^2-4}{h}\\&=&\lim_{h\to 0}\frac{4+4h+h^2-4}{h}\\&=&\lim_{h\to 0}(4+h)\\&=&4.\end{eqnarray*}

Of course, we can also use the alternative definition of $f'(a)$ to calculate the slope:\begin{eqnarray*}f'(2)&=&\lim_{x\to 2}\frac{f(x)-f(2)}{x-2}\\&=&\lim_{x\to 2}\frac{x^2-4}{x-2}\\&=&\lim_{x\to 2}\frac{(x+2)(x-2)}{x-2}\\&=&\lim_{x\to 2}(x+2)\\&=&4.\end{eqnarray*}

The equation of tangent line is then $y-4=4(x-2)$ or $y=4x-4$.

Remark. One may wonder which definition of $f'(a)$ to use. I would say that is the matter of a personal taste. For a polynomial function, one notable difference between the two definitions is that if you use the first definition, you will end up expanding a polynomial, while you will have to factorize a polynomial with the second definition. Since the expansion of a polynomial is easier than the factorization, you may want to use the first definition if you are not confident with factorizing polynomials.

Example. Find the equation of tangent line to the graph of $f(x)=x^5$ at $x=1$.

Solution. As we discussed in the previous lecture, this is an extremely difficult problem to solve by using only algebra if not impossible. But surprise! With the new method, this is more or less a piece of cake. First we calculate the slope $f'(1)$. \begin{eqnarray*}f'(1)&=&\lim_{h\to 0}\frac{(1+h)^5-1}{h}\\&=&\lim_{h\to 0}\frac{(1+h)^5-1}{h}\\&=&\lim_{h\to 0}\frac{1+5h+10h^2+10h^3+5h^4+h^5-1}{h}\\&=&\lim_{h\to 0}(5+10h+10h^2+5h^3+h^4)\\&=&5.\end{eqnarray*} Or by the second definition, \begin{eqnarray*}f'(1)&=&\lim_{x\to 1}\frac{f(x)-f(1)}{x-1}\\&=&\lim_{x\to 1}\frac{x^5-1}{x-1}\\&=&\lim_{x\to 1}\frac{(x-1)(x^4+x^3+x^2+x+1)}{x-1}\\&=&\lim_{x\to 1}(x^4+x^3+x^2+x+1)\\&=&5.\end{eqnarray*}Therefore the equation of the tangent line is given by $y-1=5(x-1)$ or $y=5x-4$. The following picture shows the graph of $y=x^5$ (in blue) and the graph of tangent line $y=5x-4$.

Let us consider a simple geometry problem. Given a curve $y=f(x)$, we want to find a line tangent to the graph of $y=f(x)$ at $x=a$ (meaning the line meets the graph of $y=f(x)$ exactly at a point $(a,f(a))$ on a small interval containing $x=a$.

One may wonder at this point why finding a tangent line is a big deal. Well, it is in fact a pretty big deal besides mathematicians’ purely intellectual curiosities. There is a reason why Sir Issac Newton had to invent calculus of which crucial notion is the slope of a tangent line. It is still too early to talk about why it is important or useful. We will get there when we are ready.

We attempt to tackle the problem with an example first. Here is an example we want to consider

Example. Find the equation of a line tangent to the graph of $y=x^2$ at $x=2$.

Solution. To find the equation of a line, we need two ingredients: slope and $y$-intercept or slope and a point. We already know a point. We know that the line must pass through $(2,4)$. So all we need to find is its slope $m$. From algebra, we know that the equation of a line passing through $(2,4)$ with slope $m$ is given by $y-4=m(x-2)$ or $y=mx-2m+4$. Since $y=x^2$ and $y=mx-2m+4$ meet exactly at one point, the quadratic equation $x^2=mx-2m+4$ or $x^2-mx+2m-4=0$ must have exactly one solution. We have learned from the theory of quadratic equations that in that case the discriminant $D=b^2-4ac$ must be equal to $0$. That is, in our case $$D=m^2-4(2m-4)=m^2-8m+16=(m-4)^2=0.$$ Hence we determine that $m=4$ and the equation of the tangent line is $y=4x-4$.

So we see that finding the slope of a tangent line is not that difficult and that it does not require any new mathematics, or does it? Remember that we have not yet tackled our problem in general context. Before we get more ambitious, consider another example with a more complicated function, say $y=x^5$. Let us say that we want to find the line tangent to the graph of $y=x^5$ at $x=1$. Then the equation of the tangent line would be $y=mx-m+1$. In order for $y=x^5$ and the line $y=mx-m+1$ to meet exactly at one point, the quintic equation $x^5-mx+m-1=0$ must have exactly one solution. Our problem here is that we have no algebraic means, such as quadratic formula or discriminant, to use to determine the value of $m$. We are stuck here and there is no hope of tackling our simple geometry problem using only algebra. That is the reason why we have to cleverly devise a new way to tackle the problem. This is where we enter the realm of Calculus. The new idea to tackle the problem is not really new and it was already used by the ancient Greeks. And the world had to wait until it was rediscovered independently by Sir Issac Newton and by Gottfried Leibniz. I do not know if any of them actually knew about the ancient Greek idea.