So far we have mainly studied finite limits. Here we would like to discuss infinite limits. You may wonder why  we need to study infinite limits. They in fact do have important applications. One immediate application is that it provides  us some information on the shape of a function, i.e. it helps us sketch the graph of a function, as we will see later.

We first begin with the notion of vertical asymptotes.

Definition. The line $x=a$ is called a  vertical asymptote of the graph of $y=f(x)$ if $$\lim_{x\to a+}f(x)=\pm\infty,\ \mbox{or}\ \lim_{x\to a-}f(x)=\pm\infty.$$

Example. Find the vertical asymptotes of the graph of $y=\displaystyle\frac{x^2-3x+2}{x^3-4x}$.

Solution. The candidates for vertical asymptotes are the values of $x$ that make the denominator $0$. In our example, they are the root of the equation $x^3-4x=0$. Since $x^3-4x=x(x^2-4)=x(x+2)(x-2)$, we find three roots $x=-2,0,2$. However, some of them may not necessarily be vertical asymptotes. To check this, we calculate the limits: \begin{eqnarray*}\lim_{x\to 0+}\frac{x^2-3x+2}{x^3-4x}&=&\frac{2}{0-}\ \mbox{(Can you see why?)}\\&=&-\infty,\\\lim_{x\to 0-}\frac{x^2-3x+2}{x^3-4x}&=&\frac{2}{0+}\\&=&\infty,\\\lim_{x\to -2-}\frac{x^2-3x+2}{x^3-4x}&=&\frac{12}{0-}\\&=&-\infty,\\\lim_{x\to -2+}\frac{x^2-3x+2}{x^3-4x}&=&\frac{12}{0+}\\&=&\infty,\\\lim_{x\to 2}\frac{x^2-3x+2}{x^3-4x}&=&\lim_{x\to 2}\frac{(x-1)(x-2)}{x(x+2)(x-2)}\\&=&\lim_{x\to 2}\frac{x-1}{x(x+2)}\\&=&\frac{1}{8}.\end{eqnarray*}

So, we see that $x=0,-2$ are vertical asymptotes while $x=2$ is not.

Definition. A line $y=b$ is called a horizontal asymptote of the graph of $y=f(x)$ if $$\lim_{x\to\infty}f(x)=b,\ \mbox{or}\ \lim_{x\to -\infty}f(x)=b.$$

Example. Find the horizontal asymptotes of the graph of $y=\displaystyle\frac{5x^2+8x-3}{3x^2+2}$.

Solution. You can notice at once that the limit $\displaystyle\lim_{x\to\infty}\frac{5x^2+8x-3}{3x^2+2}$ is an $\frac{\infty}{\infty}$ type indeterminate form. So how do we calculate this kind of indeterminate form? First divide the numerator and the denominator by the highest power of $x$ appeared in the denominator:\begin{eqnarray*}\lim_{x\to\infty}\frac{5x^2+8x-3}{3x^2+2}&=&\lim_{x\to\infty}\frac{\frac{5x^2+8x-3}{x^2}}{\frac{3x^2+2}{x^2}}\\&=&\lim_{x\to\infty}\frac{5+\frac{8}{x}-\frac{3}{x^2}}{3+\frac{2}{x^2}}\\&=&\frac{5}{3}.\end{eqnarray*} The final answer is obtained by the limits $\displaystyle\lim_{x\to\infty}\frac{1}{x^n}=0,$ where $n$ is a positive integer.

Similarly, $\displaystyle\lim_{x\to\infty}\frac{5x^2+8x-3}{3x^2+2}=\frac{5}{3}$ using the limit $\displaystyle\lim_{x\to -\infty}\frac{1}{x^n}=0,$ where $n$ is a positive integer. The following picture contains the graphs of the function (in blue) and the horizontal asymptote (in red).

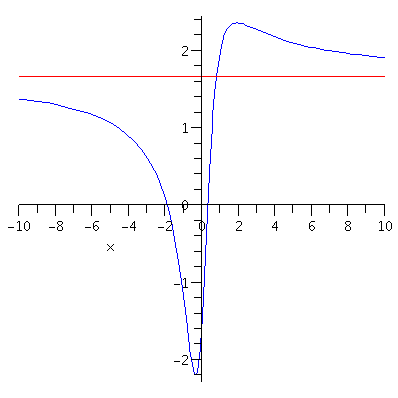
Figure 1. The graph of y=(5x^2+8x-3)/(3x^2+2)

Example. Find the horizontal asymptotes of $y=\displaystyle\frac{x^2-3x+2}{x^3-4x}$.

Solution. The limits $\displaystyle\lim_{x\to\pm\infty}\frac{x^2-3x+2}{x^3-4x}$ is $\frac{\infty}{\infty}$ type indeterminate form. So as we did in the previous example, we first divide the numerator and the denominator by the highest power of $x$ that is appeared in the denominator: \begin{eqnarray*}\lim_{x\to\infty}\frac{x^2-3x+2}{x^3-4x}&=&\lim_{x\to\infty}\frac{\frac{x^2-3x+2}{x^3}}{\frac{x^3-4x}{x^3}}\\&=&\lim_{x\to\infty}\frac{\frac{1}{x}-\frac{3}{x^2}+\frac{2}{x^3}}{1-\frac{4}{x^2}}\\&=&0.\end{eqnarray*}

Similarly you find that $\displaystyle\lim_{x\to -\infty}\frac{x^2-3x+2}{x^3-4x}=0$.

The following picture shows you the graph of the function (in blue), the horizontal and the vertical asymptotes (in red).

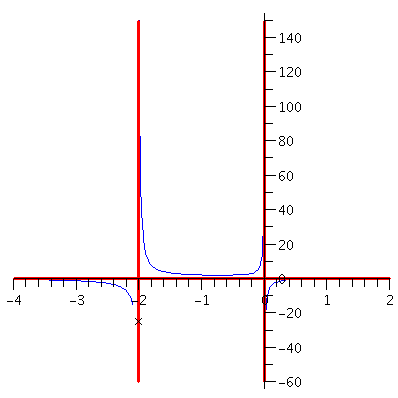
Figure 2. The graph of y=(x^2-3x+2)(x^3-4x)

Normally the graph of a function $y=f(x)$ never touches or crosses its horizontal asymptote while it gets closer and closer to its horizontal asypmtote as $x\to\infty$ or $x\to -\infty$. But there are exceptions as shown in the following example.

Example. Consider the function $f(x)=2+\displaystyle\frac{\sin x}{x}$. Using the Sandwich Theorem, one can show that $\displaystyle\lim_{x\to\pm\infty}\frac{\sin x}{x}=0$ and hence $\displaystyle\lim_{x\to\pm\infty}f(x)=2$. That is $y=2$ is a horizontal asymptote of the curve on both left and right. As you can see in the following picture, the graph crosses the horizontal asymptote $y=2$ infinitely many
times.

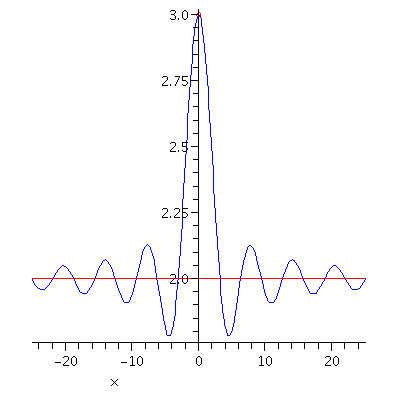
Figure 3. The graph of y=2+sin(x)/x.

There is another kind of asymptotes, called oblique (slanted) asymptotes. An oblique asymptote can be seen from a rational function $\frac{p(x)}{q(x)}$ where $\deg p(x)>\deg q(x)$. An oblique asymptote is in fact given by a dominating term of a rational function as you can see in the following example.

Example. Consider the rational function $f(x)=\displaystyle\frac{2x^2-3}{7x+4}$. By long division, we obtain \begin{eqnarray*}f(x)&=&\frac{2x^2-3}{7x+4}\\&=&\left(\frac{2}{7}x-\frac{8}{49}\right)+\frac{-115}{49(7x+4)}.\end{eqnarray*} As $x\to\pm\infty$, the remainder $\displaystyle\frac{-115}{49(7x+4)}\to 0$. Hence the graph of $f(x)$ gets closer to the graph of the linear function $y=\displaystyle \frac{2}{7}x-\frac{8}{49}$ as $x\to\pm\infty$. This linear function is an oblique (slanted) asymptote of the graph of $f(x)$. The following picture shows the graph of $f(x)$ (in blue) and both the vertical asymptote $x=-\frac{4}{7}$ and the oblique asymptote $y=\frac{2}{7}x-\frac{8}{49}$ (in red).

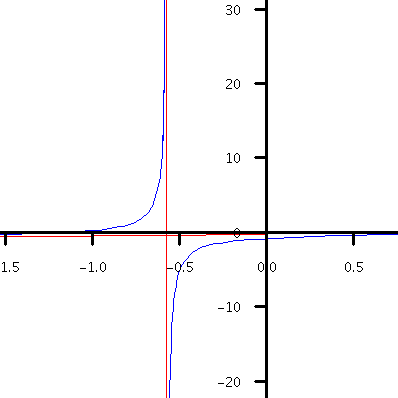
Figure 4. The graph of y=(2x^3-3)/(7x+4).

A closer look.

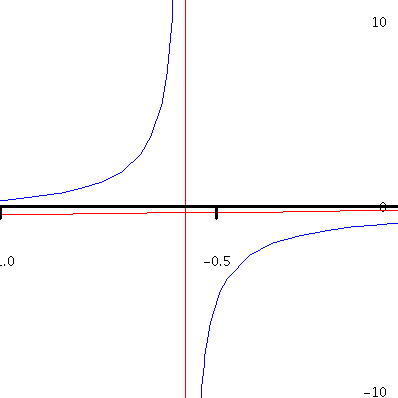
Figure 5. The graph of y=(2x^3-3)/(7x+4).