Intuitively speaking, we say a function is continuous at a point if its graph has no separation, i.e. there is no hole or breakage, at that point. Such notion of continuity can be defined explicitly as follows.

Definition: A function \(f(x)\) is said to be continuous at a point \(x=a\) if \[\lim_{x\to a}f(x)=f(a).\]

Note that the above definition assumes the existence of both \(\displaystyle\lim_{x\to a}f(x)\) and \(f(a)\).

There are 3 different types of discontinuities.

• \(f(a)\) is not defined.

For example, consider the function\[f(x)=\frac{x^2-4}{x-2}.\] Clearly \(f(2)\) is not defined. However the limit \(\displaystyle\lim_{x\to 2}f(x)\) exists:\begin{eqnarray*}\lim_{x\to 2}\frac{x^2-4}{x-2}&=&\lim_{x\to 2}\frac{(x+2)(x-2)}{x-2}\\&=&\lim_{x\to 2}(x+2)=4.\end{eqnarray*} As a result the graph has a hole.

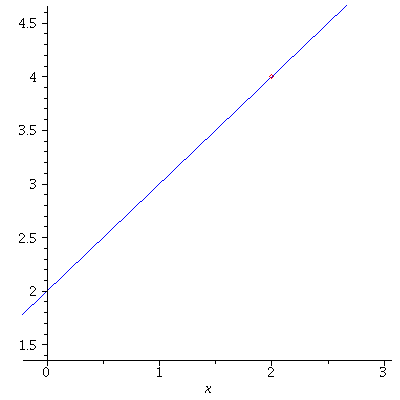This kind of discontinuity is called a removable discontinuity, meaning that we can extend \(f(x)\) to a function which is continuous at \(x=a\) in the following sense: Define \(g(x)\) by\[g(x)=\left\{\begin{array}{ccc}f(x)\ \mbox{if}\ x\ne a,\\\lim_{x\to a}f(x)\ \mbox{if}\ x=a.\end{array}\right.\]Then \(g(x)\) is a continuous at \(x=a\). The function \(g(x)\) is called the continuous extension of \(f(x)\). What we just did is basically filling the hole and the filling is the limit \(\displaystyle\lim_{x\to a}f(x)\). For the above example, we define\[g(x)=\left\{\begin{array}{ccc}\frac{x^2-4}{x-2} &\mbox{if}& x\ne 2,\\4 &\mbox{if}& x=2.\end{array}\right.\] Then \(g(x)\) is continuous at \(x=2\) and in fact, it is identical to \(x+2\).

• \(\displaystyle\lim_{x\to a}f(x)\) deos not exist.

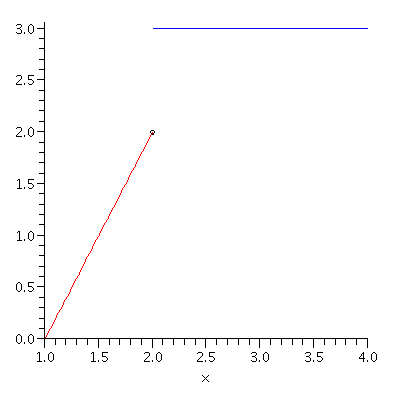
Example. Let \(f(x)=\left\{\begin{array}{cc}2x-2,\ &1\leq x<2\\3,\ &2\leq x\leq 4.\end{array}\right.\) \(f(2)=3\) but \(\displaystyle\lim_{x\to 2}f(x)\) does not exist because \(\displaystyle\lim_{x\to 2-}f(x)=2\) while \(\displaystyle\lim_{x\to 2+}f(x)=3\).

• \(f(a)\) is defined and \(\displaystyle\lim_{x\to a}f(x)\) exists, but \(\displaystyle\lim_{x\to a}f(x)\ne f(a)\).

Example. Let \(f(x)=\left\{\begin{array}{cc}\displaystyle\frac{x^2-4}{x-2},\ &x\ne 2\\3,\ &x=2.\end{array}\right.\) Then \(f(2)=3\) and \(\displaystyle\lim_{x\to 2}f(x)=4\).

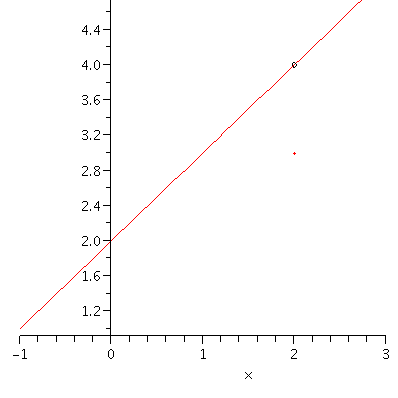
From the properties of limits (Theorem 1, Lecture 4), we obtain the following properties of continuous functions.

Theorem 9. If functions \(f(x)\) and \(g(x)\) are continuous at \(x=a\), then

1. \((f\pm g)(x)=f(x)\pm g(x)\) is continuous at \(x=a\).
2. \(f\cdot g(x)=f(x)\cdot g(x)\) is continuous at \(x=a\).
3. \(\displaystyle\frac{f}{g}(x)=\frac{f(x)}{g(x)}\) is continous at \(x=a\) provided \(g(a)\ne 0\).

There are some important classes of continous functions.

• Every polynomial function \(p(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0\) is continuous everywhere, because \(\displaystyle\lim_{x\to a}p(x)=p(a)\) for any \(-\infty<a<\infty\).
• If \(p(x)\) and \(q(x)\) are polynomials, then the rational function \(\displaystyle\frac{p(x)}{q(x)}\) is continuous wherever it is defined \(\{x\in\mathbb{R}|q(x)\ne 0\}\).
• \(y=\sin x\) and \(y=\cos x\) are continuous everywhere.
• \(y=\tan x\) is continous where it is defined, i.e. everywhere except at the points \(x=\pm\frac{\pi}{2},\pm\frac{3\pi}{2},\pm\frac{5\pi}{2},\cdots\).
• If \(n\) is a positive integer, then \(y=\root n\of{x}\) is continuous where it is defined. That is, if \(n\) is an odd integer, it is defined everywhere. If \(n\) is an even integer,it is defined on \([0,\infty)\), the set of all non-negative real numbers.

Recall that the composite function \(g\circ f(x)\) of two functions \(f(x)\) and \(g(x)\) (read \(f\) followed by \(g\)) is defined by \[g\circ f(x):=g(f(x)).\]

Theorem 10. Suppose that \(\displaystyle\lim_{x\to a}f(x)=L\) exists and \(g(x)\)is continuous function at \(x=L\). Then\[\lim_{x\to a}g\circ f(x)=g(\lim_{x\to a}f(x)).\]

It follows from Theorem 10 that the composite function of two continuous functions is again a continuous function.

Corollary 11. If \(f(x)\) is continuous at \(x=a\) and \(g(x)\) is continuous at \(f(a)\), the the composite function \(g\circ f(x)\) is continuous at \(x=a\).

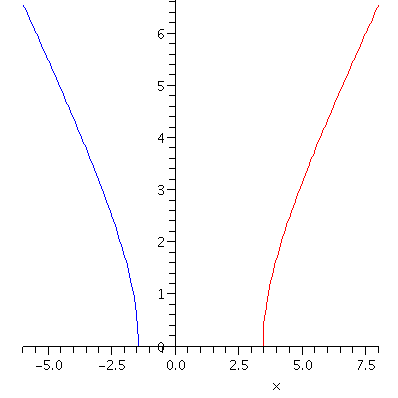
Example. The function\(y=\sqrt{x^2-2x-5}\) is the composite function  \(g\circ f(x)\) of two functions \(f(x)=x^2-2x-5\) and \(g(x)=\sqrt{x}\). The function \(f(x)=x^2-2x-5\) is continuous everywhere while \(g(x)=\sqrt{x}\) is continuous on \([0,\infty)\), so by Corollary 11, the composite function \(g\circ f(x)=\sqrt{x^2-2x-5}\) is continuous on its repective domain which is \((-\infty,1-\sqrt{6}]\) or \([1+\sqrt{6},\infty)\). The following picture shows you the graph of \(y=\sqrt{x^2-2x-5}\) on the intervals  \((-\infty,1-\sqrt{6}]\) and \([1+\sqrt{6},\infty)\).

Continuous functions exhibit many nice properties. I would like to introduced a couple of them here. The first is the so-called Max-Min Theorem.

Theorem 12. [Max-Min Theorem] If \(f(x)\) is a continuous function on a closed interval \([a,b]\), \(f(x)\) attains its maximum value and minimum value on \([a,b]\).

Another important property is the so-called Intermediate Value Theorem (IVT). The IVT has an important application in the study of equations.

Theorem 13. [The Intermediate Value Theorem] If \(f(x)\) is continuous on a closed interval \([a,b]\) and \(f(a)\ne f(b)\), then , then \(f(x)\) takes on every value between \(f(a)\) and \(f(b)\). In other words, if \(f(a)<k<f(b)\) (assuming that \(f(a)<f(b)\)), then \(f(c)=k\) for some number \(a<c<b\).

It follows from Theorem 13 that

Corollary 14. If \(f(x)\) is continuous on a closed interval \([a,b]\) and \(f(a)\cdot f(b)<0\), then \(f(x)=0\) for some \(a<x<b\).

Using  Corollary 14 we can tell if a root of the equation \(f(x)=0\) can be found in some interval. For instance

Example. Show that the equation \(x^3-x-1=0\) has a root in the interval \([-1,2]\).

Solution. Let \(f(x)=x^3-x-1\). Then \(f(x)\) is continuous on \([-1,2]\). Since \(f(-1)=-1\) and \(f(2)=5\) have different signs, by Corollary 14 there is a root of \(x^3-x-1=0\) in the open interval \((-1,2)\).