In mathematics and also in applications, we often encounter problems that require to maximize or minimize the value of a certain quantity. The general procedure can be summarized as:

1. Express the quantity to be maximized or minimized in terms of a single variable. The quantity may be described in terms of two variables however with given constraint it could be reduced to a single variable.
2. Differentiate the function obtained in step 1 and set the derivative equal to 0.
3. Solve the equation from step 2 to obtain critical values and determine whether they maximize or minimize the given quantity. Usually the first or second derivative test is a convenient tool for the required inspection.

Example. A farmer has 2400 ft of fencing and wants to fence off a rectangular field that borders a straight river. He needs no fence along the river. What are the dimensions of the field that has the largest area?

Solution. Let $x$ and $y$ denote the length and the width of the rectangular field. Suppose that the side along the river has the length $x$. Then the area is $A=xy$ and the required fencing in terms $x$ and $y$ is $x+2y=2400$. This fencing is a constraint and solve it for $y$ to obtain $y=1200-\frac{x}{2}$. Plugging this into $A$ for $y$, the area can be written as a function of a single variable $x$: $$A(x)=1200x-\frac{x^2}{2}$$ $A'(x)=1200-x$ and setting this equal to 0, we find $x=1200$. Since $A^{\prime\prime}(x)=-1<0$, by the second derivative test $x=1200$ gives rise to the absolute maximum of $A(x)$. The required dimensions are $1200\ \mbox{ft}\times 600\ \mbox{ft}$ where the side that borders the river is 1200 ft and the resulting largest area is 720,000 $\mbox{ft}^2$.

Example. A box with a square base and open top must have a volume of 32,000 $\mbox{cm}^3$. Find the dimensions of the box that minimize the amount of material used.

Solution. Let $x$ and $h$ be the length and the height of the box, respectively. Then $x^2h=32000$ and we want to minimize the surface area $A=x^2+4xh$. Solve the volume constraint for $h$ to obtain $h=\frac{32000}{x^2}$. Plugging this into $A$ for $h$, we write $A$ as a function of a single variable $x$: $$A(x)=x^2+\frac{128000}{x}$$ $A'(x)=2x-\frac{128000}{x^2}$ and setting it equalto 0, we find $x=40$. Since $A^{\prime\prime}(x)=2+\frac{256000}{x^3}>0$ for all $x>0$, $A(40)$ is the absolute minimum. Therefore the required dimensions are $40\ \mbox{cm}\times 40\ \mbox{cm}\times 20\ \mbox{cm}$.

Example. If 1200 $\mbox{cm}^2$ of material is available to make a box with a square base and an open top, find the largest possible volume of the box.

Solution. Let $x$ and $h$ be the length and the height of the box, respectively. Then $x^2+4xh=1200$ and we want to maximize $V=x^2h$. Solve the area for $h$ to obtain $h=\frac{1200-x^2}{4x}$. Plugging this into $V$, we write the volume as a function of a single variable $x$: $$V(x)=300x-\frac{1}{4}x^3$$ $V'(x)=300-\frac{3}{4}x^2$ and setting it equal to 0, we find $x=20$. Since $V'(x)$ is a quadratic polynomial with a negative leading coefficient, $V(20)=4000\ \mbox{cm}^3$ is the largest possible volume of the box.

Example. Find the point on the parabola $y^2=2x$ that is the closest to the point $(1,4)$.

Solution. Let $(x,y)$ denote a point on the parabola $y^2=2x$. The distance between $(x,y)$ and $(1,4)$ is $d=\sqrt{(x-1)^2+(y-4)^2}$ and we want to minimize this. Note minimizing $d$ is equivalent to minimizing $d^2=(x-1)^2+(y-4)^2$. Solve the equation of parabola for $x$ to obtain $x=\frac{y^2}{2}$. Plugging this into $d^2$, we can write it as a function of a single variable $y$: $$f(y)=\left(\frac{y^2}{2}-1\right)^2+(y-4)^2=\frac{y^4}{4}-8y+17$$ $f'(y)=y^3-8$ and setting it equal to 0, we find $y=2$. Since $f^{\prime\prime}(y)=3y^2>0$ for all $y\ne 0$, $(x,y)=(2,2)$ is the point on the parabola $y^2=2x$ that is the closest to $(1,4)$.

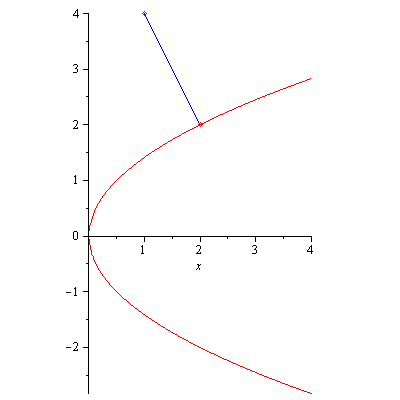
Remark. The above problem also can be solved using a simple geometric fact that the shortest path from $(1,4)$ to the parabola $y^2=2x$ would be normal to the tangent line (i.e. the path is perpendicular to the tangent line). Let $(a,b)$ be the point on the parabola that is closest to $(1,4)$. By implicit differentiation we find $\frac{dy}{dx}=\frac{1}{y}$ and so the normal line at $(a,b)$ has the slope $-b$. The equation of the normal line is then $y-4=-b(x-1)$. Since this line is passing through $(a,b)$, $b-a=-b(a-1)$ or $ab=4$. $(a,b)$ is also on the parabola so we have $b^2=2a$. Solve the two equations simultaneously to obtain $b=2$ and hence $a=2$. Therefore, $(a,b)=(2,2)$.

Example. An open box is to be made out of a 6-inch by 18-inch piece of cardboard by cutting out squares of equal size from the four corners and bending up the sides. Find the dimensions of the resulting box that has the largest volume.

Solution. When you tackle this type of problems, it is very important to draw a picture that properly depicts the description of the problem as shown in the following figure.

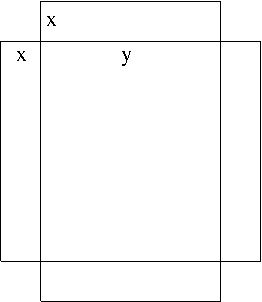
From the figure, the length and the width of the box are, respectively, $18-2x$ and $y=6-2x$. Thus, the volume $V$ is $$V(x)=(6-2x)(18-2x)x=4x^3-48x^2+108x$$ To find the critical points, set $$V'(x)=12x^2-96x+108=0$$ or equivalently $x^2-8x+9=0$. This quadratic equation has two solutions $x=4\pm\sqrt{7}$. Recall that in order for a critical point $c$ to maximize the volume, it is required that $$V^{\prime\prime}(c)=24c-96<0,$$ i.e. $c<4$. Thus, $x=4-\sqrt{7}=1.35425$ maximizes the volume $V(x)$. The dimensions of the box that has the largest volume is then $$15.2915\times 3.2915$$

Example. A fence 4 feet tall runs parallel to a tall building at a distance of 2 feet from the building. What is the length of the shortest ladder that will reach from the ground over the fence to the wall of the building?

Solution. The following figure depicts the description of the problem.

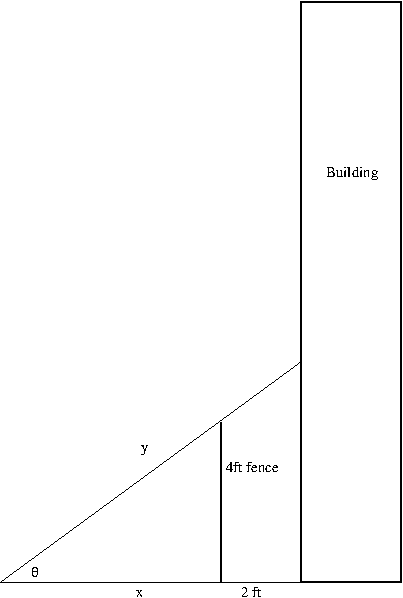
The big and small right triangles are similar triangles, so we have $$\frac{x+2}{y}=\frac{x}{\sqrt{x^2+16}}$$ which is equal to $\cos\theta$. Solving the equation for $y$, we obtain $$y=\sqrt{x^2+16}+\frac{2\sqrt{x^2+16}}{x}$$ To minimize $y$, we find $$y’=\frac{x^3-32}{x^2\sqrt{x^2+16}}$$ and there is only one critical point $x=\root 3\of{32}=2\root 3\of{4}$. The resulting $y$ value, i.e. the length of the shortest ladder is then $8.32388$. By the second derivative, one can confirm that the critical point indeed minimizes the length of the ladder. But even without using the second derivative, one can make the length of such ladder as long as one likes, so there is no maximum length of such ladder.