Let $y=f(x)$ and $y=g(x)$ be continuous functions on a closed interval $[a,b]$ such that $f(x)\geq g(x)$ on $[a,b]$ as shown in Figure 1.

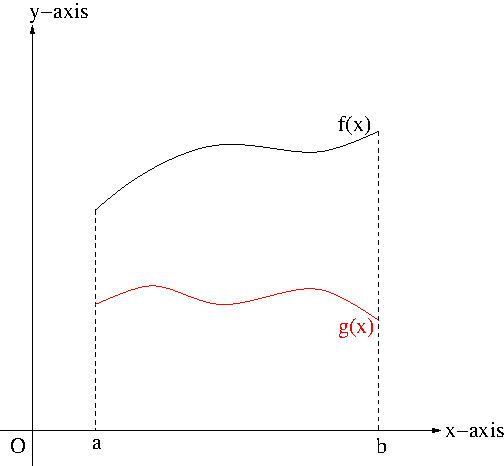
Figure 1

If the region bounded by $f(x)$ and $g(x)$ on $[a,b]$ is revolved about the $x$-axis, the volume of the resulting solid is obtained by \begin{align*}V&=\int_a^b\pi [f(x)]^2dx-\int_a^b\pi [g(x)]^2dx\\&=\int_a^b\pi ([f(x)]^2-[g(x)]^2)dx\end{align*} This is essentially the disk method but it is rather called the washer method because each cross section is a washer due to a hollow core within the solid.

Example. The region bounded by  the curve $y=x^2+1$ and the line $y=-x+3$ is revolved about the $x$-axis. Find the volume of the resulting solid.

Solution. Figure 2 shows the bounded region

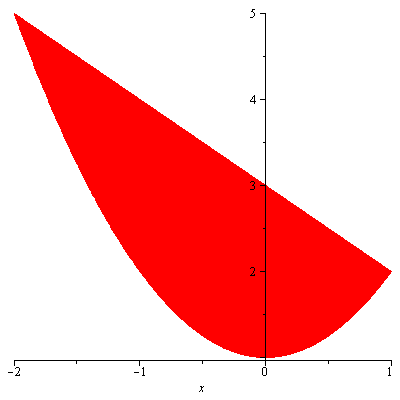
Figure 1

and Figure 2 shows the solid of revolution.

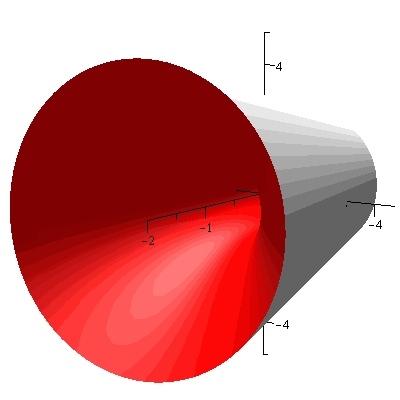
Figure 2

The volume $V$ is given by $$V=\int_{-2}^1\pi[(-x+3)^2-(x^2+1)^2]dx=\frac{117\pi}{5}$$

Example. The region bounded by the parabola $y=x^2$ and the line $y=2x$ in the first quadrant is revolved about the $y$-axis to generate a solid. Find the volume of the solid.

Solution. Figure 3 shows the bounded region

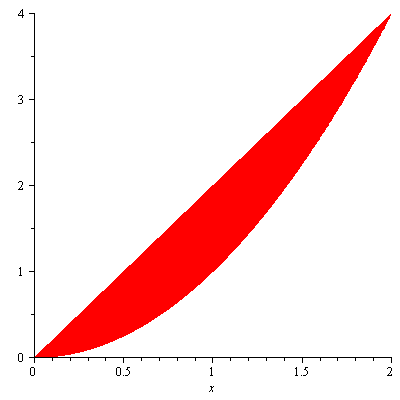
Figure 3

and Figure 4 shows the solid of revolution.

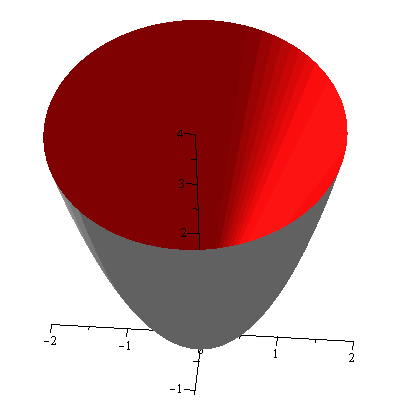
Figure 4

The volume of the solid is given by $$V=\int_0^4\pi\left[(\sqrt{y})^2-\left(\frac{y}{2}\right)^2\right]dy=\frac{8\pi}{3}$$