Let $y=f(x)$ and $y=g(x)$ be two continuous functions on a closed interval $[a,b]$ such that $f(x)\geq g(x)$ on $[a,b]$ as seen in Figure 1.

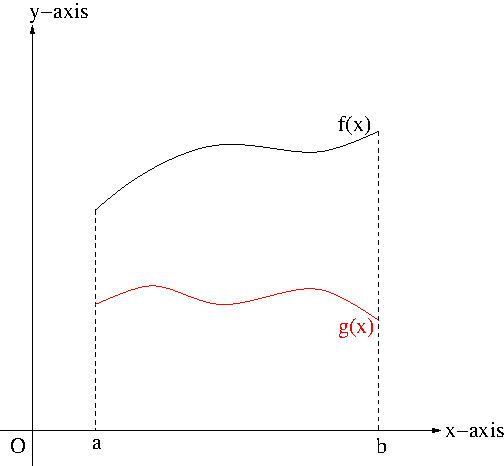
Figure 1

The area $A$ of the region between the curves $f(x)$ and $g(x)$ is \begin{align*}A&=\int_a^b f(x)dx-\int_a^b g(x)dx\\&=\int_a^b[f(x)-g(x)]dx\end{align*}

Example. Find the area of the region enclosed by the parabola $y=2-x^2$ and the line $y=-x$.

Solution. First we need to find the $x$-coordinates of the points at which the two curves meet. Set $2-x^2=-x$. Then the quadratic equation $x^2-x-2=0$ has two solutions $x=-1,2$. From Figure 2

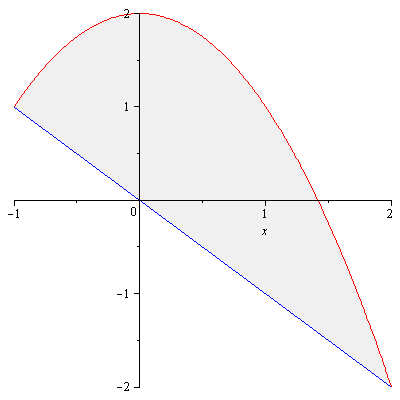
Figure 2

we see that the area is \begin{align*}A&=\int_{-1}^2[(2-x^2)-(-x)]dx\\&=\int_{-1}^2(2+x-x^2)dx\\&=\frac{9}{2}\end{align*}

Example. Find the area of the region in the first quadrant that is bounded above by $y=\sqrt{x}$ and below by the $x$-axis and the line $y=x-2$.

Solution. To find the $x$-coordinates of the points at which $y=\sqrt{x}$ and $y=x-2$ meet, set $\sqrt{x}=x-2$. Squaring this equation, we obtain the quadratic equation $x^2-5x+4=0$ whose solutions are $x=-1$ and $x=4$. Since we are considering only the first quadrant $x=-1$ is not our concern. The bounded region is shown in Figure 3.

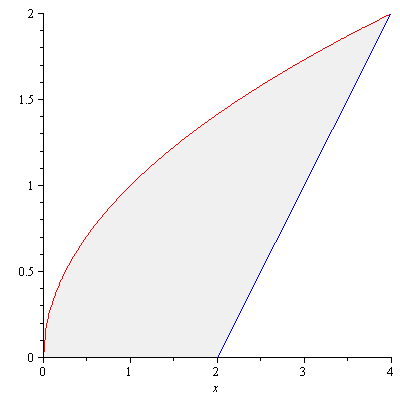
Figure 3

Note that on $[0,2]$ the part of the region is bounded by $y=\sqrt{x}$ and the $x$-axis and on $[2,4]$ the part of the reagion is bounded by $y=\sqrt{x}$ and $y=x-2$. Hence, the area is \begin{align*}A&=\int_0^2\sqrt{x}dx+\int_2^4[\sqrt{x}-(x-2)]dx\\&=\frac{10}{3}\end{align*}

If $x=f(y)$ and $x=g(y)$ are two continuous functions on a closed interval $[c,d]$ such that $f(y)\geq g(y)$ as seen in Figure 4,

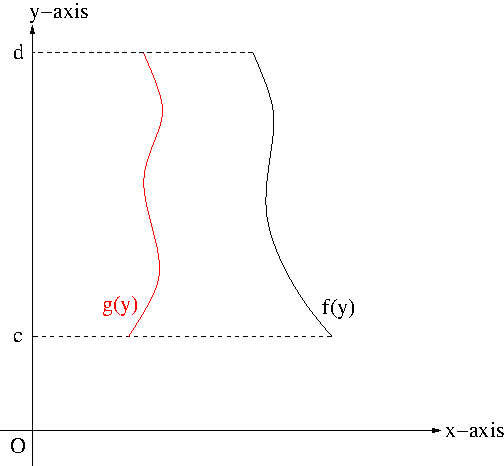
Figure 4

then the area $A$ bounded by $f(y)$ and $g(y)$ is given by $$A=\int_c^d[f(y)-g(y)]dy$$

Example. Redo the previous example by integrating with respect to $y$.

Solution. The same region in Figure 3 can be considered as the region bounded by $x=y^2$ ($y\geq 0$ and $x=y+2$. Hence, $$A=\int_0^2[y+2-y^2]dy=\frac{10}{3}$$

Often the fastest way to find an area may be to combine calculus with geometry. The same region in Figure 3 can be viewed as in Figure 5.

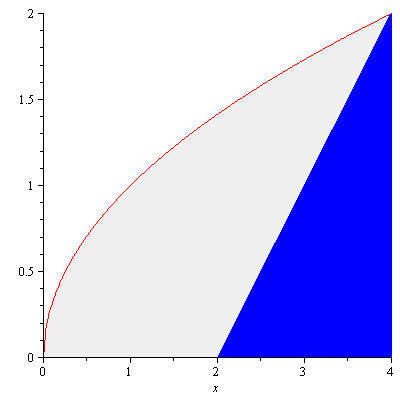
Figure 5

The area of the right triangle in blue is $\frac{1}{2}\cdot 2\cdot 2=2$ hence, the area of the region is $$A=\int_0^4\sqrt{x}dx-2=\frac{10}{3}$$