Disk Method

Consider the solid obtained by rotating a region bounded by the function $y=f(x)$ and the $x$-axis, $a\leq x\leq b$.

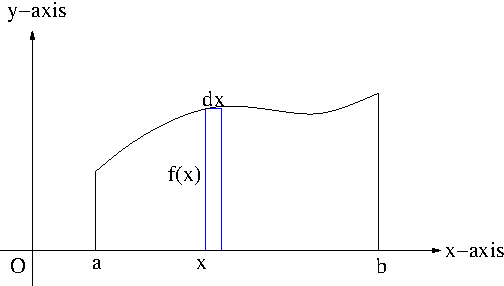
Figure 1

The cross section of the resulting sold at $x$ is a disk of radius $f(x)$ as seen in Figure 1 and so its area is $A(x)=\pi [f(x)]^2$. Hence the volume of the solid of revolution is \begin{equation}\label{eq:diskmethod}V=\pi\int_a^b [f(x)]^2dx\end{equation}

Example. The region between the curve $y=\sqrt{x}$, $0\leq x\leq 4$ and the $x$-axis is revolved about the $x$-axis. Find the volume of the resulting solid.

Solution. Figure 2 shows the region

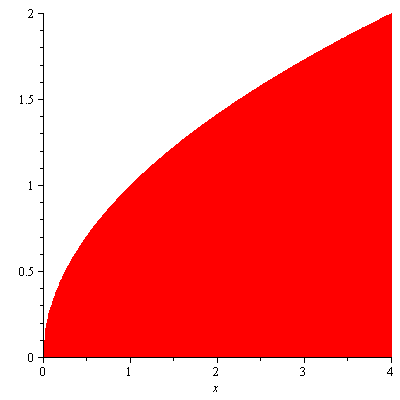
Figure 2

and Figure 3 shows the resulting solid.

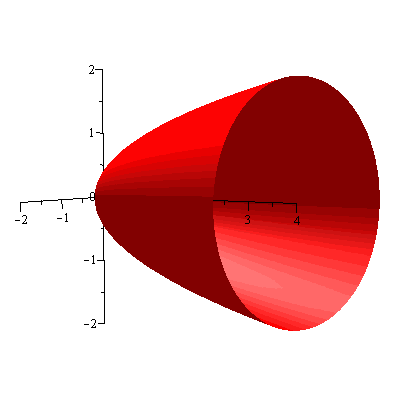
Figure 3

The volume $V$ is given by $$V=\pi\int_0^4[\sqrt{x}]^2dx=\pi\int_0^4 xdx=8\pi$$

Example. Find the volume of the solid generated by revolving the region bounded by $y=\sqrt{x}$ and the lines $y=1$, $x=4$ about the line $y=1$.

Solution. Figure 4 shows the region

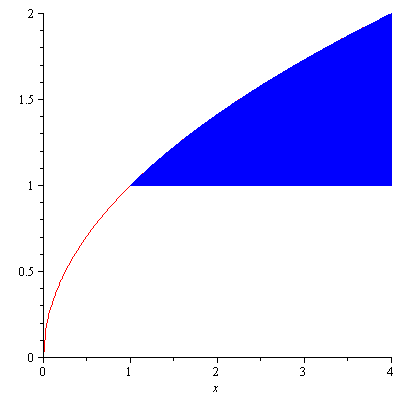
Figure 4

and Figure 5 shows the resulting solid.

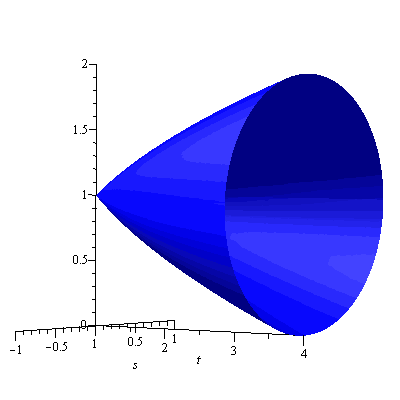
Figure 5

Note that the radius of the cross section at $x$ is $\sqrt{x}-1$ and so the volume is given by $$V=\pi\int_1^4[\sqrt{x}-1]^2dx=\frac{7}{6}\pi$$

Example. Find the volume of the solid obtained by revolving the region between the $y$-axis and the curve $x=\frac{2}{y}$, $1\leq y\leq 4$ about the $y$-axis.

Solution. Figure 6 shows the region

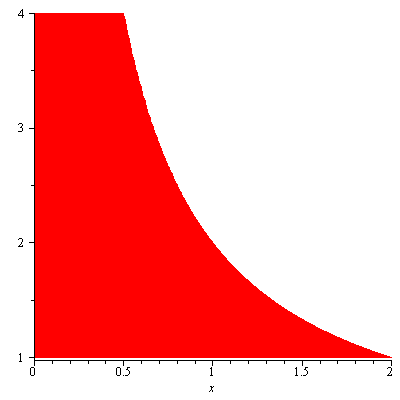
Figure 6

and Figure 7 shows the resulting solid.

Figure 7

The area of the cross section at $y$ is $A(y)=\pi\left(\frac{2}{y}\right)^2$. Hence the volume is $$V=\int_1^4 A(y)dy=\pi\int_1^4\left(\frac{2}{y}\right)^2dy=3\pi$$