A function $y=f(x)$ is said to be one-to-one if satisfies the property
$$f(x_1)=f(x_2) \Longrightarrow x_1=x_2$$
or equivalently
$$x_1\ne x_2 \Longrightarrow f(x_1)\ne f(x_2)$$
for all $x_1,x_2$ in the domain. In plain English what this says is no two numbers in the domain are corresponded to the same number in the range. Figure 1 is the graph of $f(x)=x^2$. It is not one-to-one.

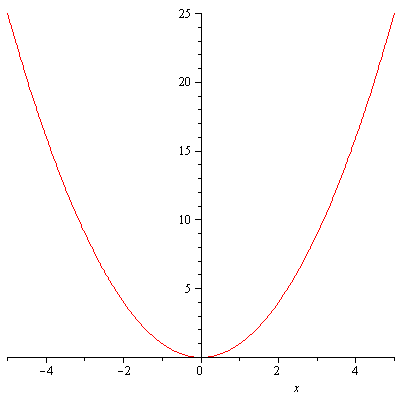
Figure 1. The graph of y=x^2

For example, $-1\ne 1$ but $f(-1)=1=f(1)$.

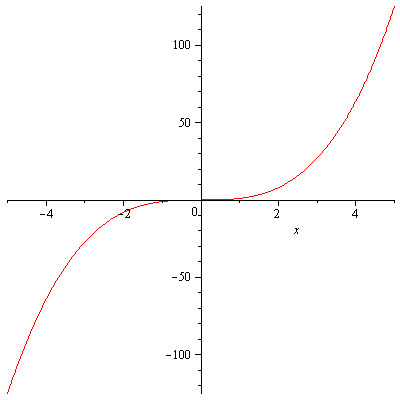
Figure 2. The graph of y=x^3

Figure 2 is the graph of $f(x)=x^3$. It is one-to-one as seen clearly from the graph. But let us pretend that we don’t know the graph but want to prove that it is one-to-one following the definition. Here we go. Suppose that $f(x_1)=f(x_2)$. Then $x_1^3=x_2^3$ or $x_1^3-x_2^3=(x_1-x_2)(x_1^2+x_1x_2+x_2^2)=0$. This means $x_1=x_2$ which completes the proof.

Why do we care about one-to-one functions? The reason is that if $y=f(x)$ is one-to-one, it has an inverse function $y=f^{-1}(x)$.
\begin{align*}
x&\stackrel{f}{\longrightarrow} y\\
x&\stackrel{f^{-1}}{\longleftarrow} y
\end{align*}
Given a one-to-one function $y=f(x)$, here is how to find its inverse function $y=f^{-1}(x)$

STEP 1. Swap $x$ and $y$ in $y=f(x)$. The reason we are doing this is that $\mathrm{Dom}(f)=\mathrm{Range}(f^{-1})$ and $\mathrm{Dom}(f^{-1})=\mathrm{Range}(f)$.

STEP 2. Solve the resulting expression $x=f(y)$ for $y$. That is the inverse function $y=f^{-1}(x)$.

Example. Find the inverse function of $f(x)=\frac{2x+3}{x-1}$. (It is a one-to-one function.)

Solution. STEP 1. Let $y=\frac{2x+3}{x-1}$ and swap $x$ and $y$. Then we have
$$x=\frac{2y+3}{y-1}$$

STEP 2. Let us solve $x=\frac{2y+3}{y-1}$ for $y$. First multiply $x=\frac{2y+3}{y-1}$ by $y-1$. Then we have $x(y-1)=2y+3$ or $xy-x=2y+3$. Isolating the terms that contain $y$ in the LHS, we get $xy-2y=x+3$ or $(x-2)y=x+3$. Finally we find $y=\frac{x+3}{x-2}$. This is the inverse function.

$y=f(x)$ and its inverse $y=f^{-1}(x)$ satisfy the following properties.
$$(f\circ f^{-1})(x)=x,\ (f^{-1}\circ f)(x)=x$$
The reason for these properties to hold is clear from the definition of an inverse function. We can check the properties using the above example. I will do $(f\circ f^{-1})(x)=x$ and leave the other for an exercise.
\begin{align*}
(f\circ f^{-1})(x)&=f(f^{-1}(x))\\
&=f\left(\frac{x+3}{x-2}\right)\\
&=\frac{2\left(\frac{x+3}{x-2}\right)+3}{\left(\frac{x+3}{x-2}\right)-1}\\
&=x
\end{align*}
The graph of $y=f(x)$ and the graph of its inverse $y=f^{-1}(x)$ satisfy a nice symmetry, namely they are symmetric about the line $y=x$. This symmetry helps us obtain the graph of $y=f^{-1}(x)$ when the explicit expression for $f^{-1}(x)$ is not available. You will see such a case later when you study the logarithmic functions. Figure 3 shows the symmetry with $y=x^2$ ($x\geq 0$) and its inverse $y=\sqrt(x)$.

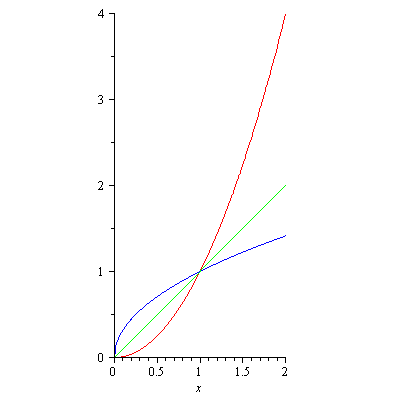
Figure 3. The symmetry between the graphs of y=x^2 (red) and y=sqrt(x) (blue) about y=x (green)