A line in the plane is determined by two points meaning there is only one line passing through two given points in the plane. But it could be determined by some other quantities. An important such quantity is slope. Slope measures steepness of a line and it is defined by $\frac{\mbox{rise}}{\mbox{run}}$. If two points $(x_1,y_1)$ and $(x_2,y_2)$ are known, the slope $m$ of the line through the two points is
\begin{equation}
\label{eq:slope}
m=\frac{y_2-y_1}{x_2-x_1}
\end{equation}

Example. Find the slope of the line passing through the points $P(2,1)$ and $Q(8,5)$.

Solution. Note that it really doesn’t matter which ones you label as $(x_1,y_1)$ and $(x_2,y_2)$. Here we choose $(x_1,y_1)=(2,1)$ and $(x_2,y_2)=(8,5)$. Using \eqref{eq:slope} we find the slope
$$m=\frac{5-1}{8-2}=\frac{4}{6}=\frac{2}{3}$$

A cool thing to see is that certain geometric objects can be described by equations so we can study geometry in terms of algebra. Such objects include lines, circles, parabolas, elipses, and so on so forth. Why is this cool? Because algebra is much easier than geometry. A branch of mathematics that studies geometric objects in terms of algebra is analytic geometry and this is further generalized into another branch called algebraic geometry.

So how do we write an equation for a given line? Well, we already have it. The equation \eqref{eq:slope}. But in order to write it as an equation we need to tweak it a bit. An equation relates an arbitrary point $(x,y)$ on the line to some known quantities. So let’s say slope $m$ and a point $(x_1,y_1)$ is known. Then by \eqref{eq:slope} we get
$$m=\frac{y-y_1}{x-x_1}$$
This is the equation of the line with slope $m$ passing through a point $(x_1,y_1)$. But to make it look a bit nicer we rewrite it as
\begin{equation}
\label{eq:line}
y-y_1=m(x-x_1)
\end{equation}

Example. Find the equation of the line through $(-1,3)$ with slope $-\frac{1}{2}$ and sketch the line.

Solution. Using \eqref{eq:line} we find
$$y-3=-\frac{1}{2}(x-(-1))$$
Solving this for $y$ we obtain
$$y=-\frac{1}{2}x+\frac{5}{2}$$
There are two ways to sketch the line. One is using the slope and the given point. Slope being $-\frac{1}{2}$ means that when $x$ moves 2 units to the right its corresponding $y$ moves 1 unit downward. Apply this to the point $(-1,3)$ we will land at another point which is $(1,2)$. You draw the line passing through the two points $(-1,3)$ and $(1,2)$ as shown in Figure 1.

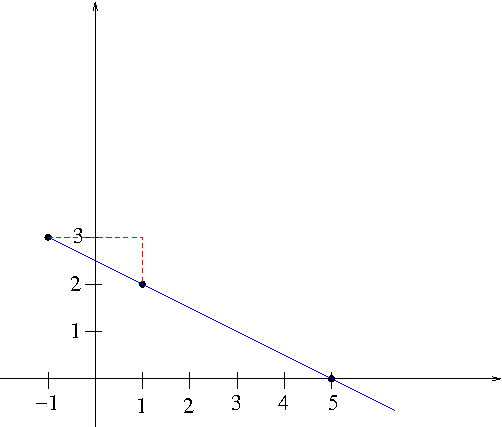
Figure 1. Drawing a line

The other way to sketch the line is to find another point. An easy choice is to find the $x$-intercept by setting $y=0$. The $x$-intercept is $(5,0)$. You draw the line through $(-1,3)$ and $(5,0)$.

As a special case if the slope $m$ and the $y$-intercept $(0,b)$ are given, the equation \eqref{eq:line} becomes
\begin{equation}
\label{eq:line2}
y=mx+b
\end{equation}
Even though the $y$-intercept is not known in fact \eqref{eq:line2} can be also used to find the equation of the line in the previous example. Since $m=-\frac{1}{2}$, we set
$$y=-\frac{1}{2}x+b$$
The line is passing through $(-1,3)$ we have
$$3=-\frac{1}{2}(-1)+b$$
Solving this for $b$ we find $b=\frac{5}{2}$.

Parallel and Perpendicular Lines

It’s obvious that two lines with slopes $m_1$ and $m_2$ are parallel if $m_1=m_2$. What’s not so obvious however is the following property.

Two lines with slopes $m_1$ and $m_2$ are perpendicular if $m_1m_2=-1$.

We will not mind the proof of this property here.

Example. Find an equation of the line through $(5,2)$ that is parallel to the line $y=-\frac{2}{3}x-\frac{5}{6}$.

Solution. The slope is $m=-\frac{2}{3}$. Since this line is passing through the point $(5,2)$, by \eqref{eq:line} the equation is
$y-2=-\frac{2}{3}(x-5)$. This simplifies to
$y=-\frac{2}{3}x+\frac{16}{3}$.

Example. Find an equation of the line through $(5,2)$ that is perpendicular to the line $y=-\frac{2}{3}x-\frac{5}{6}$.

Solution. The slope is $m=\frac{3}{2}$. Since the line is passing through $(5,2)$, by \eqref{eq:line} the equation is
$y-2=\frac{3}{2}(x-5)$ which simplifies to $y=\frac{3}{2}x-\frac{11}{2}$.

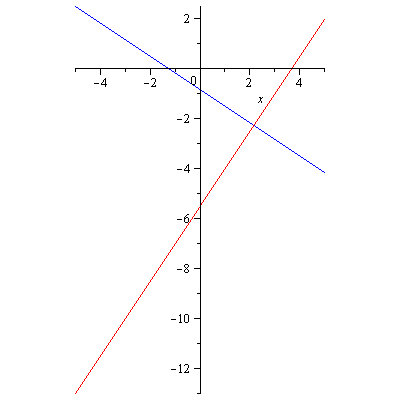
Figure 2. Two perpendicular lines y=-(2/3)x-5/6 (in blue) and y=(3/2)x-11/2 (in red)