From here on, I assume a background of undergraduate level Linear Algebra. Readers should be familiar with notions such as vector spaces, subspaces, linear combination, linear dependence and linear independence, basis, and dimension.
In this lecture, we begin with the notion of a normed space. A normed space is a vector space with a norm defined. So what is a norm? A norm $||\cdot||$ is a real-valued function $||\cdot||: V\longrightarrow\mathbb{R}^+\cup\{0\}$ such that for $x,y\in V$ and for $\alpha$ a scalar,
(N1) $||x||=0\Longleftrightarrow x=O$.
(N2) $||\alpha x||=|\alpha|||x||$.
(N3) $||x+y||\leq ||x||+||y||$. (Triangle Inequality.)
A norm on $V$ defines a metric $d$ on $V$
\begin{equation}
\label{eq:metric}
d(x,y)=||x-y||.
\end{equation}
\eqref{eq:metric} is called a metric induced by the norm $||\cdot||$. So, a normed space is a metric space but the converse need not be true.
A complete normed space is called a Banach space.
Example. $\mathbb{R}^n$ and $\mathbb{C}^n$ with the Euclidean norm
$$||x||=\left(\sum_{j=1}^n|\xi_j|^2\right)^{\frac{1}{2}}$$ are Banach spaces.
Example. $\ell^p$ with the norm
$$||x||=\left(\sum_{j=1}^n|\xi_j|^p\right)^{\frac{1}{p}}$$ is a Banach space.
Example. $\ell^\infty$ with the norm
$$||x||=\sup_{j\in\mathbb{N}}|\xi_j|$$ is a Banach space.
Example. $\mathcal{C}[a,b]$ with the norm
$$||x||=\max_{t\in[a,b]}|x(t)|$$ is a Banach space.
What follows next is an example of a normed space which is not complete. $\mathcal{C}[a,b]$, the vector space of all continuous real-valued functions on $[a,b]$ forms a normed space with the norm defined by
\begin{equation}
\label{eq:intnorm}
||x||=\left(\int_a^b x(t)^2dt\right)^{\frac{1}{2}}.
\end{equation}
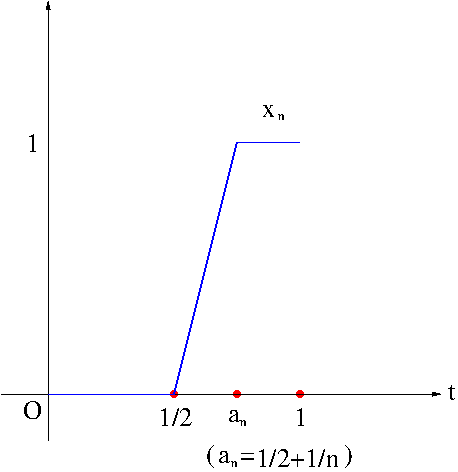
Let $[a,b]=[0,1]$. for each $n=1,2,\cdots$, let $a_n=\frac{1}{2}+\frac{1}{n}$. Define a sequence $(x_n)$ in $\mathcal{C}[0,1]$ by
$$x_n(t)=\left\{\begin{array}{ccc}
0 & \mbox{if} & t\in\left[0,\frac{1}{2}\right],\\
nt-\frac{n}{2} & \mbox{if} & t\in\left[\frac{1}{2},a_n\right],\\
1 & \mbox{if} & t\in[a_n,1].
\end{array}\right.$$
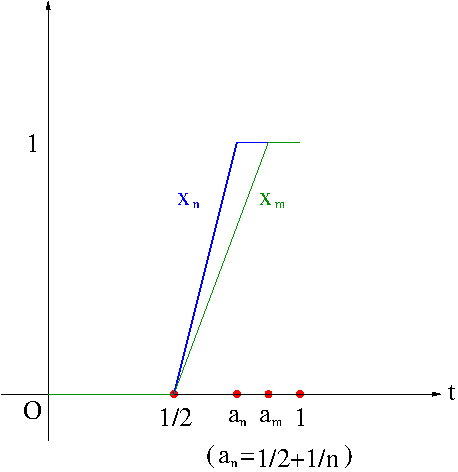 Let us assume that $n>m$. Then
Let us assume that $n>m$. Then
\begin{align*}
||x_m-x_n||^2&=\int_0^1(x_m(t)-x_n(t))^2dt\\
&=\int_0^{\frac{1}{2}}(x_m(t)-x_n(t))^2dt+\int_{\frac{1}{2}}^{a_n}(x_m(t)-x_n(t))^2dt\\&+\int_{a_n}^{a_m}(x_m(t)-x_n(t))^2dt+\int_{a_m}^1(x_m(t)-x_n(t))^2dt\\
&=\int_{\frac{1}{2}}^{\frac{1}{2}+\frac{1}{n}}\left(nt-\frac{n}{2}-mt+\frac{m}{2}\right)^2dt+\int_{\frac{1}{2}+\frac{1}{n}}^{\frac{1}{2}+\frac{1}{m}}\left(1-mt+\frac{m}{2}\right)^2dt\\
&=\frac{(n-m)^2}{3mn^2}\\
&<\frac{1}{3m}-\frac{1}{3n}.
\end{align*}
Given $\epsilon>0$, choose a positive integer $N$ so that $N>\frac{1}{3\epsilon^2}$. Then for all $m,n\geq N$,
\begin{align*}
||x_n-x_m||^2&<\frac{1}{3m}-\frac{1}{3n}\\
&<\frac{1}{3m}\\
&\leq\frac{1}{3N}\\
&<\epsilon^2.
\end{align*}
Therefore, $(x_n)$ is a Cauchy sequence in $\mathcal{C}[0,1]$. For any $x(t)\in\mathcal{C}[0,1]$,
\begin{align*}
||x_n-x||^2&=\int_0^1(x_n(t)-x(t))^2dt\\
&=\int_0^{\frac{1}{2}}x(t)^2dt+\int_{\frac{1}{2}}^{a_n}(x_n(t)-x(t))^2dt+\int_{a_n}^1(1-x(t))^2dt.
\end{align*}
Suppose that $x_n\rightarrow x$ as $n\to\infty$. The by the continuity of $x_n(t)$ and $x(t)$, $x(t)$ must satisfy that
$$x(t)=\left\{\begin{array}{ccc}
0 & \mbox{if} & t\in\left[0,\frac{1}{2}\right),\\
1 & \mbox{if} & t\in\left(\frac{1}{2},1\right].
\end{array}\right.$$
But this is impossible since $x(t)$ is continuous. Hence, $(x_n)$ is not convergent in $\mathcal{C}[0,1]$.
In here, we studied completion of metric spaces. Since a normed space is a metric space, we also have completion of normed spaces. The completion of $\mathcal{C}[a,b]$ with the norm \eqref{eq:intnorm} is denoted by $L^2[a,b]$. More generally, for any $p\geq 1$, the Banach space $L^p[a,b]$ is the completion of the normed space $\mathcal{C}[a,b]$ with the norm
\begin{equation}
||x||_p=\left(\int_a^b|x(t)|^pdt\right)^{\frac{1}{p}}.
\end{equation}
Lemma. A metric $d$ induced by a norm on a normed space $X$ satisfies
- $d(x+a,y+a)=d(x,y)$, $a,x,y\in X$. This means that $d$ is translation invariant.
- $d(\alpha x,\alpha y)=|\alpha|d(x,y)$, $\alpha$, a scalar.
Proof.
\begin{align*}
d(x+a,y+a)&=||x+a-(y+a)||=||x-y||=d(x,y),\\
d(\alpha x,\alpha y)&=||\alpha x-\alpha y||=|\alpha|||x-y||=|\alpha|d(x,y).
\end{align*}
We know that a norm on a vector space $V$ defines a metric on $V$. Can every metric on a vector space $V$ be obtained from a norm? The answer is negative. Let $V$ be the set of all bounded or unbounded sequences of complex numbers. Then $V$ is a vector space. The metric $d$ on $V$ defined by
$$d(x,y)=\sum_{j=1}^\infty\frac{1}{2^j}\frac{|\xi_j-\eta_j|}{1+|\xi_j-\eta_j|}$$ is not translation invariant, so it cannot be obtained from a norm.
