Nonlinear Inequalities

Leave a reply

Nonlinear inequalities may seem more complicated and difficult to solve than linear inequalities. However it is not really the case. There is one simple way to solve a nonlinear inequality. It’s called the test point method. I will explain this with an example.

Example. Solve the inequality $x^2\leq 5x-6$.

Solution. The inequality can be rewritten $x^2-5x+6\leq 0$. First we find points at which $x^2-5x+6=0$. Since $x^2-5x+6=(x-2)(x-3)$, $x=2,3$. These two points divide the real line into 3 regions, where $x<2$, where $2<x<3$, and where $x>3$ as shown in Figure 1.

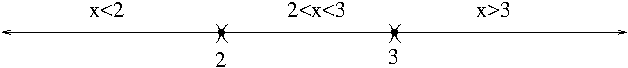
Figure 1. Quadratic Inequality

In each region we pick a test point to see if that test number satisfies the given inequality. If it does, any other number in the same region would satisfy the inequality. If not, any other number in the same region wouldn’t either. While this is pretty cool, you may wonder why this works. One number speaks for the entire numbers in the same region. It’s hard to explain here though but it is due to the continuity of the function $f(x)=x^2-5x+6$. I will leave it at that and will not delve into that any further. You will understand what I said when you learn calculus. In the region $x<2$, I would pick $x=0$ for a test point. But $x=0$ won’t satisfy the inequality as the LHS is $6>0$. Move onto the next region $2<x<3$. I pick $x=2.5=\frac{5}{2}$. Since $\left(\frac{5}{2}\right)^2-5\frac{5}{2}+6=\frac{25-50+24}{4}=-\frac{1}{4}<0$. So this means that $2<x<3$ is a solution of the inequality. In the final region $x>3$ I pick $x=4$. $(4)^2-5(4)+6=2>0$ so no number in this region would satisfy the inequality. Since $x=2$ and $x=3$ also satisfy the inequality, the overall solution is $2\leq x\leq 3$ or $[2,3]$ in interval notation.

The inequalities like one we just did is called quadratic inequalities. For quadratic inequalities we can actually classify solutions depending on inequalities without going through the test point method every time. Let us assume that the quadratic function $f(x)=ax^2+bx+c$ with $a>0$ has two real solutions $\alpha$ and $\beta$ ($\alpha<\beta$). Then the graph of $f(x)$ would look like one in Figure 2. You can find the solution of each of the following quadratic inequalities easily from the graph in Figure 2.

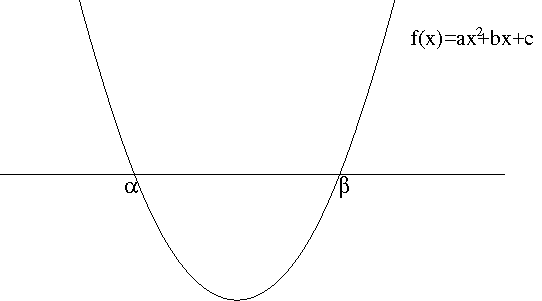
Figure 2. Quadratic Inequality

  1. $ax^2+bx+c>0$: $x<\alpha$ or $x>\beta$. In interval notation, $(-\infty,\alpha)\cup(\beta,\infty)$.
  2. $ax^2+bx+c\geq 0$: $x\leq\alpha$ or $x\geq\beta$. In interval notation, $(-\infty,\alpha]\cup[\beta,\infty)$.
  3. $ax^2+bx+c<0$: $\alpha<x<\beta$. In interval notation, $(\alpha,\beta)$.
  4. $ax^2+bx+c\leq 0$: $\alpha\leq x\leq\beta$. In interval notation, $[\alpha,\beta]$.

Let us go over a couple more examples of nonlinear inequalities that are not quadratic inequalities.

Example. Solve $x(x-1)^2(x-3)<0$.

Solution. The method is the same as the first example. We use the test point method. First find $x$ at which $x(x-1)^2(x-3)=0$. They are $x=0, 1, 3$. So there are 4 regions under consideration. $x<0$, $0<x<1$, $1<x<3$, and $x>3$. In the region where $x<0$, the test point $x=-1$ results the sign of the LHS is $+$. So $x<0$ is not a solution. In the region $0<x<1$, the test point $x=\frac{1}{2}$ results the sign of the LHS $-$, so $0<x<1$ is a solution. In the region $1<x<3$, the test point $x=2$ results the sign of the LHS still $-$. This is actually due to $(x-1)^2$. In general if you see an even number of repeated term $x-a$ in your polynomial inequality like the one we have the sign of the polynomial does not change at $x=a$. A little goody to know so you can save time. Let us move onto next and last one. For $x>3$ the test point $x=4$ results the sign of the LHS $+$, so $x>3$ is not a solution. Therefore, the overall solution is $0<x<1$ or $1<x<3$. In interval notation, it is $(0,1)\cup(1,3)$.

Example. Solve $\frac{1+x}{1-x}\geq 1$.

Solution. First rewrite the inequality as $\frac{1+x}{1-x}-1\geq 0$ which simplifies to $\frac{2x}{1-x}\geq 0$. Inequality like this we consider points at which the numerator is 0 and also points at which the denominator is 0. In our case they are $x=0, 1$ and these two points divide the real line into three regions: $x<0$, $0<x<1$, $x>1$. In the region $x<0$, the test point $x=-1$ results the sign of the LHS $-$, so $x<0$ is not a solution. In the region $0<x<1$, the test point $x=\frac{1}{2}$ results the sign of the LHS $+$, so $0<x<1$ is a solution. Finally in the region $x>1$ the test point $x=2$ results the sign of the LHS $-$, so $x>1$ is not a solution. Since $x=0$ also satisfies the inequality, the overall solution is $0\leq x<1$ or $[0,1)$ in interval notation.

Lorentz Invariance of Relativistic Equations

Leave a reply

Relativistic equations are the equations whose solutions describe certain relativistic motions. Such equations include wave equation, Klein-Gordon equation, Dirac equation etc. A relativistic equation must describe the same physical motion independent of frames i.e. whether an observer is in a frame at rest or in a frame moving at the constant speed $v$. For this reason, all those relativistic equations are required to be invariant under the Lorentz transformation. We show that the wave equation
\begin{equation}
\label{eq:waveeq}
-\frac{1}{c^2}\frac{\partial^2\psi}{\partial t^2}+\frac{\partial^2\psi}{\partial x^2}=0
\end{equation}
is Lorentz invariant. Here we consider only 1-dimensional wave equation for simplicity. Wave equation has two kinds of solutions. Given boundary conditions its solution describes a vibrating string in which case the boundary conditions are the ends of the string that are held fixed. This is called Fourier’s solution. The other type can be obtained by not imposing any boundary conditions. The resulting solution would describe a propagating wave in vacuum spacetime. Such a propagating wave includes electromagnetic waves. Light is also an electromagnetic wave. This is called a d’Alembert’s solution. The proof is easy. All that’s required is the chain rule.

First let us recall the Lorenz transformation
$$t’=\frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}},\ x’=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}$$
Using the chain rule we find
\begin{align*}
\frac{\partial}{\partial x}&=\frac{\partial}{\partial x’}\frac{\partial x’}{\partial x}+\frac{\partial}{\partial t’}\frac{\partial t’}{\partial x}\\
&=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\frac{\partial}{\partial x’}-\frac{v}{c^2\sqrt{1-\frac{v^2}{c^2}}}\frac{\partial}{\partial t’}\\
\frac{\partial}{\partial t}&=\frac{\partial}{\partial x’}\frac{\partial x’}{\partial t}+\frac{\partial}{\partial t’}\frac{\partial t’}{\partial t}\\
&=-\frac{v}{\sqrt{1-\frac{v^2}{c^2}}}\frac{\partial}{\partial x’}+\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\frac{\partial}{\partial t’}
\end{align*}
Applying the chain rule again,
\begin{align*}
\frac{\partial^2}{\partial x^2}&=\frac{1}{1-\frac{v^2}{c^2}}\frac{\partial^2}{\partial {x’}^2}+\frac{v^2}{c^4\left(1-\frac{v^2}{c^2}\right)}\frac{\partial^2}{\partial {t’}^2}-2\frac{v}{c^2\left(1-\frac{v^2}{c^2}\right)}\frac{\partial^2}{\partial t’\partial x’}\\
\frac{\partial^2}{\partial t^2}&=\frac{v^2}{1-\frac{v^2}{c^2}}\frac{\partial^2}{\partial {x’}^2}+\frac{1}{1-\frac{v^2}{c^2}}\frac{\partial^2}{\partial {t’}^2}-2\frac{v}{1-\frac{v^2}{c^2}}\frac{\partial^2}{\partial t’\partial x’}
\end{align*}
It follows that
$$-\frac{1}{c^2}\frac{\partial^2\psi}{\partial t^2}+\frac{\partial^2\psi}{\partial x^2}=-\frac{1}{c^2}\frac{\partial^2\psi}{\partial {t’}^2}+\frac{\partial^2\psi}{\partial {x’}^2}$$
Therefore, the wave equation is Lorentz invariant.

Would the wave equation be invariant under the Galilean transformation? The answer is no. Recall the Galilean transformation
$$t’=t,\ x’=x-vt$$
We find that under the Galiean transformation
$$-\frac{1}{c^2}\frac{\partial^2\psi}{\partial t^2}+\frac{\partial^2\psi}{\partial x^2}=-\frac{1}{c^2}\frac{\partial^2\psi}{\partial {t’}^2}+\left(1-\frac{v^2}{c^2}\right)\frac{\partial^2\psi}{\partial {x’}^2}+\frac{2v}{c^2}\frac{\partial^2\psi}{\partial t’\partial x’}$$
Hence obvisouly the wave equation is not invariant under the Galiean transformation. This implies that there is no light in Euclidean space.

Food for Thought. You can also show that the heat equation (1-dimensional)
$$-\frac{\partial u}{\partial t}+\alpha\frac{\partial^2 u}{\partial x^2}=0$$
is not Lorentz invariant. Is there any relativistic version of the heat equation? There are models of relativistic heat conduction but in my opinion they are more like mathematically augmented equations rather than they are derived in a physically meaningful way. So my question is can we derive a physically meaningful equation of relativistic heat conduction? One may wonder if there is actually any physical phenomenon that exhibits a relativistic heat conduction. As far as I know there isn’t any observed one yet. I speculate though that one may observe a relativistic heat conduction from an extreme physical phenomenon such as a quasar jet.

Update: Of course the Lorentz invariance can be also shown using the Lorentz transformation \begin{align*}t’&=\cosh\phi t-\sinh\phi x\\x’&=-\sinh\phi t+\cosh\phi x\end{align*}

Update: For 3-dimensional case the wave equation is given by $$\Box\psi=0$$
where $\Box=-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}+\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$ is the d’Alembert’s operator. This case is actually simpler to show its Lorentz invariance. Note $\Box=\nabla\cdot \nabla$ where $\nabla=\frac{1}{c}\frac{\partial}{\partial t}\hat e_0+\frac{\partial}{\partial x}\hat e_x+\frac{\partial}{\partial y}\hat e_2+\frac{\partial}{\partial z}\hat e_3$. Since $\nabla$ is a 4-vector (rigorously it is not a vector but an operator but can be treated as a vector), its squared norm $\Box$ has to be Lorentz invariant.

Absolute Value Equations and Absolute Value Inequalities

Leave a reply

Absolute Value Equations

First let us review the definition of absolute value $|\cdot |$.

Definition. The absolute value of $|a|$ of a number $a$ is defined by
$$|a|=\left\{\begin{array}{ccc}
a & \mbox{if} & a\geq 0\\
-a & \mbox{if} & a<0
\end{array}\right.$$
Interestingly a lot of students get confused with the definition while they have no problem with getting the absolute of a particular number correctly like $|2|=2$ and $|-2|=2$. That’s because of the way they were taught. Many teachers teach absolute value like some sort of magic: “Hey guys what absolute value does is whatever number you put into between the two vertical lines it becomes positive.” While this may be easy to understand for students this is not an action performed in mathematics. In algebra whatever action you do should be carried out by operations such as $+$, $-$, $\times$, or $\div$. In terms of an operation what happens to $|-2|=2$ is in fact that $|-2|=-(-2)=2$. It is not abracadabra. For a letter $a$ representing a number, if $a<0$, to make it positive $|a|=-a$. Students get confused because $-a$ looks like negative but it is not. Remember the condition $a<0$. So $-a$ is actually positive. So don’t be deceived by its look.

Now we are ready to discuss absolute value equations. All you need to know is
\begin{equation}
\label{eq:abs}
|x|=k\ \mbox{if and only if}\ x=\pm k
\end{equation}
for $k>0$. If $k=0$, $x=0$. If $k<0$, obviously there is no solution.

Example. Solve the equation
$$|2x-5|=3$$

Solution. By \eqref{eq:abs}, we get the two linear equations $2x-5=\pm 3$. Solving these equation, we find $x=4$ or $x=1$.

Absolute value equations are related to quadratic equations. If you square the above equation, we get the quadratic equation
$$x^2-5x+4=0$$
Solving this quadratic equation, we of course obtain the same solutions. In practice why bother? Solving absolute value equations directly is easier. Note though that absolute value equations are actually obtained when you solve quadratic equations by the method of completing the square.

Absolute Value Inequalities

For absolute value inequalities all you have to know is the following picture.

Figure 1. Absolute Value Inequalities

From Figure 1 we can read for $k>0$

  1.  $|x|<k$ if and only if $-k<x<k$.
  2. $|x|\leq k$ if and only if $-k\leq x\leq k$.
  3. $|x|>k$ if and only if $x<-k$ or $x>k$.
  4. $|x|\geq k$ if and only if $|x|\leq -k$ or $|x|\geq k$.

Example. Solve the inequality $|x-5|<2$.

Solution. $|x-5|<2$ implies that $-2<x-5<2$ i.e. $3<x<7$.

Example. Solve the inequality $|3x+2|\geq 4$.

Solution. $|3x+2|\geq 4$ implies that $3x+2\leq -4$ or $3x+2\geq 4$ i.e. $x\leq-2$ or $x\geq\frac{2}{3}$.

Lorentz Transformation 3

1 Reply

Let $\begin{pmatrix}
t\\
x
\end{pmatrix}$ be a vector in $tx$-plane and $\begin{pmatrix}
t’\\
x’
\end{pmatrix}$ denote its rotation by a hyperbolic angle $\phi$. Then as we have seen here we have:
\begin{equation}
\begin{aligned}
t’&=t\cosh\phi-x\sinh\phi\\
x’&=-t\sinh\phi+x\cosh\phi
\end{aligned}\label{eq:boost1}
\end{equation}
$t’$-axis ($x’=0$) is moving at a constant speed
\begin{equation}
\label{eq:velocity1}
v=\frac{x}{t}=\frac{\sinh\phi}{\cosh\phi}=\tanh\phi\end{equation}
while $x’$-axis ($t’=0$) is moving at a constant speed
\begin{equation}
\label{eq:velocity2}
v=\frac{x}{t}=\frac{\cosh\phi}{\sinh\phi}=\coth\phi
\end{equation}
This means that the time and spacial axes scissor together and hence the speed of light remains the same regardless of the coordinate transformation as illustrated in Figure 1. The picture in Figure 1 is called the spacetime diagram.

Figure 1. Spacetime Diagram

From Euclidean perspective, $t’$ and $x’$ do not appear to be orthogonal. However, from Lorentzian perspective they are orthogonal. To see that let $e_0=\begin{pmatrix}
1\\
0 \end{pmatrix}$ and $e_1=\begin{pmatrix}
0\\
1
\end{pmatrix}$. Also let $e_0’$ and $e_1’$ be the rotations of $e_0$ and $e_1$ by the hyperbolic angle $\phi$, respectively. Then by \eqref{eq:boost1} we have
$$e_0’=\begin{pmatrix}
\cosh\phi\\
-\sinh\phi
\end{pmatrix},\ e_1’=\begin{pmatrix}
-\sinh\phi\\
\cosh\phi
\end{pmatrix}$$
Now \begin{align*}\langle {e_0}’,e_1’\rangle&=(\cosh\phi\ -\sinh\phi)\begin{pmatrix}
-1 & 0\\
0 & 1
\end{pmatrix}\begin{pmatrix}
-\sinh\phi\\
\cosh\phi
\end{pmatrix}\\&=\cosh\phi\sinh\phi-\sinh\phi\cosh\phi=0\end{align*} So $e_0’$ and $e_1’$ are orthogonal.

\eqref{eq:boost1} with \eqref{eq:velocity1} can be written as
\begin{align*}
t’&=\cosh\phi(t-vx)\\
x’&=\cosh\phi(x-vt)
\end{align*}
Using the well-known identy $\cosh^2\phi-\sinh^2\phi=1$, we find $\cosh\phi=\frac{1}{\sqrt{1-v^2}}$. Therefore, \eqref{eq:boost1} can be written in terms of $t,x,t’,x’,v$ as
\begin{equation}
\begin{aligned}
t’&=\frac{t-vx}{\sqrt{1-v^2}}\\
x’&=\frac{x-vt}{\sqrt{1-v^2}}
\end{aligned}\label{eq:boost2}
\end{equation}
Remember that we assumed the speed of light to be $c=1$ for simplicity. For the real $c$ value \eqref{eq:boost2} turns into
\begin{equation}
\begin{aligned}
t’&=\frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}}\\
x’&=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}
\end{aligned}\label{eq:boost3}
\end{equation}
In physics textbooks, \eqref{eq:boost3} is introduced as the Lorentz transformation. If $v\ll c$ meaning $v$ is significantly slower than the speed of light (such a motion is called a non-relativistic motion), \eqref{eq:boost3} is effectively the Galilean transformation
\begin{equation}
\begin{aligned}
t’&=t\\
x’&=x-vt
\end{aligned}\label{eq:galilean}
\end{equation}
for Newtonian mechanics in Euclidean space. $t’=t$ means that time is independent of the relative motion of different observers and we already know this is the case of Newtonian mechanics. The Galilean transformation \eqref{eq:galilean} can be also obtained by taking the limit $c\to \infty$. This indicates that in Newtonian mechanics the speed of light is presumed to be infinity.

Lines

Leave a reply

A line in the plane is determined by two points meaning there is only one line passing through two given points in the plane. But it could be determined by some other quantities. An important such quantity is slope. Slope measures steepness of a line and it is defined by $\frac{\mbox{rise}}{\mbox{run}}$. If two points $(x_1,y_1)$ and $(x_2,y_2)$ are known, the slope $m$ of the line through the two points is
\begin{equation}
\label{eq:slope}
m=\frac{y_2-y_1}{x_2-x_1}
\end{equation}

Example. Find the slope of the line passing through the points $P(2,1)$ and $Q(8,5)$.

Solution. Note that it really doesn’t matter which ones you label as $(x_1,y_1)$ and $(x_2,y_2)$. Here we choose $(x_1,y_1)=(2,1)$ and $(x_2,y_2)=(8,5)$. Using \eqref{eq:slope} we find the slope
$$m=\frac{5-1}{8-2}=\frac{4}{6}=\frac{2}{3}$$

A cool thing to see is that certain geometric objects can be described by equations so we can study geometry in terms of algebra. Such objects include lines, circles, parabolas, elipses, and so on so forth. Why is this cool? Because algebra is much easier than geometry. A branch of mathematics that studies geometric objects in terms of algebra is analytic geometry and this is further generalized into another branch called algebraic geometry.

So how do we write an equation for a given line? Well, we already have it. The equation \eqref{eq:slope}. But in order to write it as an equation we need to tweak it a bit. An equation relates an arbitrary point $(x,y)$ on the line to some known quantities. So let’s say slope $m$ and a point $(x_1,y_1)$ is known. Then by \eqref{eq:slope} we get
$$m=\frac{y-y_1}{x-x_1}$$
This is the equation of the line with slope $m$ passing through a point $(x_1,y_1)$. But to make it look a bit nicer we rewrite it as
\begin{equation}
\label{eq:line}
y-y_1=m(x-x_1)
\end{equation}

Example. Find the equation of the line through $(-1,3)$ with slope $-\frac{1}{2}$ and sketch the line.

Solution. Using \eqref{eq:line} we find
$$y-3=-\frac{1}{2}(x-(-1))$$
Solving this for $y$ we obtain
$$y=-\frac{1}{2}x+\frac{5}{2}$$
There are two ways to sketch the line. One is using the slope and the given point. Slope being $-\frac{1}{2}$ means that when $x$ moves 2 units to the right its corresponding $y$ moves 1 unit downward. Apply this to the point $(-1,3)$ we will land at another point which is $(1,2)$. You draw the line passing through the two points $(-1,3)$ and $(1,2)$ as shown in Figure 1.

Figure 1. Drawing a line

The other way to sketch the line is to find another point. An easy choice is to find the $x$-intercept by setting $y=0$. The $x$-intercept is $(5,0)$. You draw the line through $(-1,3)$ and $(5,0)$.

As a special case if the slope $m$ and the $y$-intercept $(0,b)$ are given, the equation \eqref{eq:line} becomes
\begin{equation}
\label{eq:line2}
y=mx+b
\end{equation}
Even though the $y$-intercept is not known in fact \eqref{eq:line2} can be also used to find the equation of the line in the previous example. Since $m=-\frac{1}{2}$, we set
$$y=-\frac{1}{2}x+b$$
The line is passing through $(-1,3)$ we have
$$3=-\frac{1}{2}(-1)+b$$
Solving this for $b$ we find $b=\frac{5}{2}$.

Parallel and Perpendicular Lines

It’s obvious that two lines with slopes $m_1$ and $m_2$ are parallel if $m_1=m_2$. What’s not so obvious however is the following property.

Two lines with slopes $m_1$ and $m_2$ are perpendicular if $m_1m_2=-1$.

We will not mind the proof of this property here.

Example. Find an equation of the line through $(5,2)$ that is parallel to the line $y=-\frac{2}{3}x-\frac{5}{6}$.

Solution. The slope is $m=-\frac{2}{3}$. Since this line is passing through the point $(5,2)$, by \eqref{eq:line} the equation is
$y-2=-\frac{2}{3}(x-5)$. This simplifies to
$y=-\frac{2}{3}x+\frac{16}{3}$.

Example. Find an equation of the line through $(5,2)$ that is perpendicular to the line $y=-\frac{2}{3}x-\frac{5}{6}$.

Solution. The slope is $m=\frac{3}{2}$. Since the line is passing through $(5,2)$, by \eqref{eq:line} the equation is
$y-2=\frac{3}{2}(x-5)$ which simplifies to $y=\frac{3}{2}x-\frac{11}{2}$.

Figure 2. Two perpendicular lines y=-(2/3)x-5/6 (in blue) and y=(3/2)x-11/2 (in red)