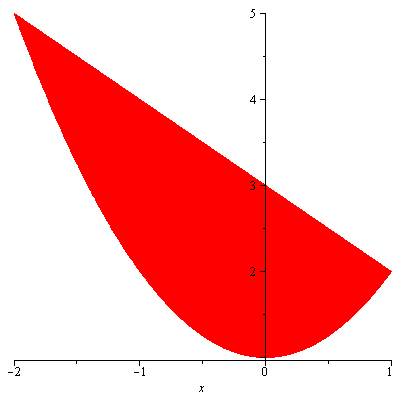
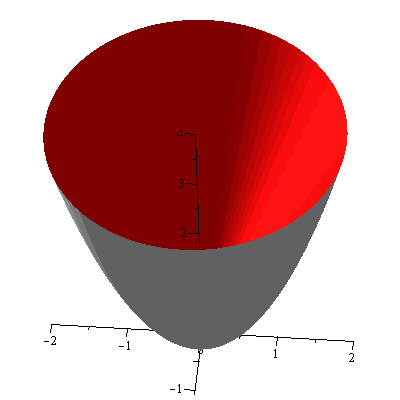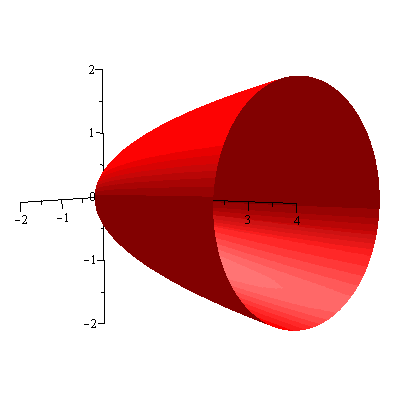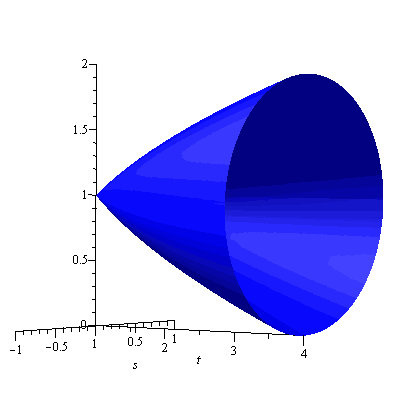Suppose that the region bounded by $y=x^4+1$, $x$-axis, $x=1$ and $x=2$, as shown in Figure 1, is revolved about the $y$-axis and we want to find the volume of the resulting solid.
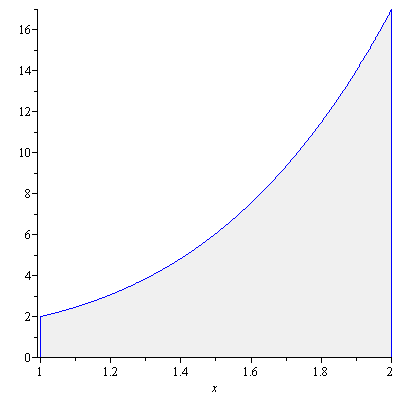
Figure 1
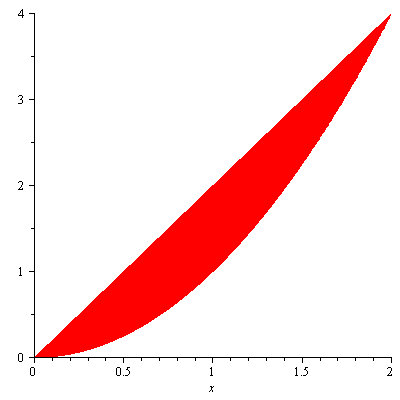
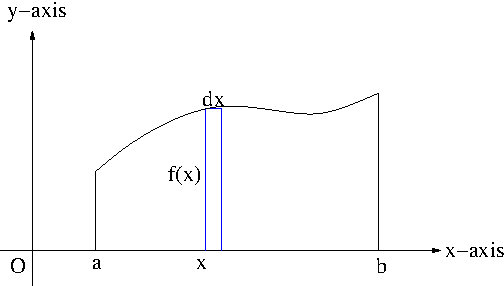
You will find it difficult to apply the disk method or the washer method for this though it’s doable. Here we want to devise another method that can come in handy for this kind of problems. First let us take a look at Figure 2.
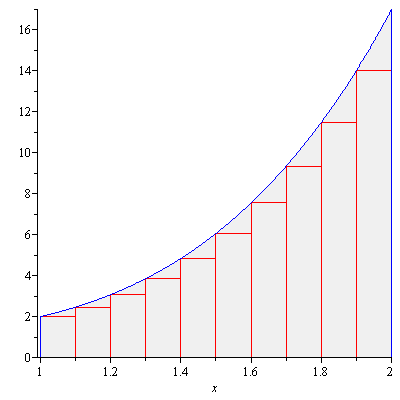
Figure 2
Imagine that each rectangle is rotated about the $y$-axis. Then we would obtain layers of cylindrical shells and the sum of the volumes of these cylindrical shells would approximate the volume of the solid in question. If we use infinitesimally thin rectangles, the sum of the volumes of cylindrical shells would be exactly the volume of the solid. The radius of the cylindrical shell at $x$ is $x$ since the axis of rotation is the $y$-axis ($x=0$), its height is $x^4+1$, and its infinitesimal thickness is $dx$. So the volume of the cylindrical shell at $x$ is $2\pi x(x^4+1)dx$. Therefore the volume of the solid is $$V=\int_1^2 2\pi x(x^4+1)dx=24\pi$$
Example. Find the volume of the solid formed by rotating the region enclosed by $$x=0,\ x=1,\ y=0,\ y=9+x^3$$ about the $y$-axis.
Solution.
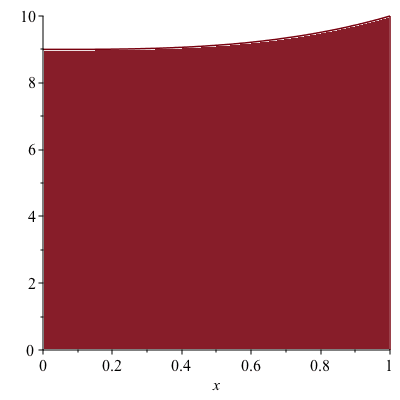
Figure 3
The enclosed region is shown in Figure 3. Using the cylindrical shell method, the volume is \begin{align*}V&=\int_0^1 2\pi x(9+x^3)dx\\&=2\pi\int_0^1(9x+x^4)dx\\&=2\pi\left[\frac{9}{2}x^2+\frac{x^5}{5}\right]_0^1\\&=\frac{47}{5}\pi\end{align*}
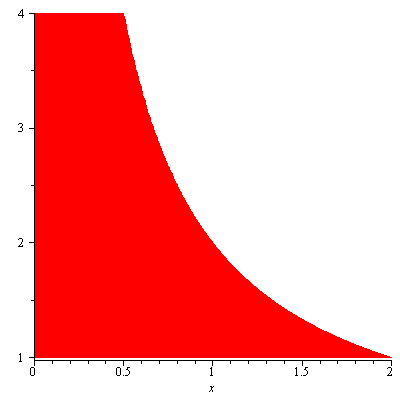
Remark. The volume can be also found by the disk/washer method but its solution is more complicated than the one by cylindrical shell method. In order to use the disk/washer method, we need to break the enclosed region into two parts as shown in Figure 4.
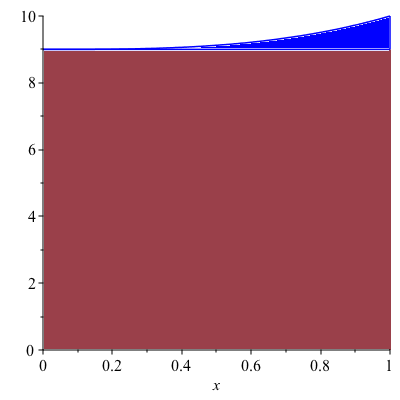
Figure 4
When rotated about the $y$-axis, the region in red will give rise to a solid cylinder with the radius 1 and the height 9. Its volume is $9\pi$. For the solid formed by rotating the region in blue, using the washer method, its volume is given by \begin{align*}\int_9^{10}\pi [1^2-((y-9)^{\frac{1}{3}})^2]dy&=\pi\int_9^{10}[1-(y-9)^{\frac{2}{3}}]dy\\&=\pi\left[y-\frac{3}{5}(y-9)^{\frac{5}{3}}\right]_9^{10}\\&=\frac{2}{5}\pi\end{align*} Therefore, the volume $V$ of the solid in question is given by $$V=9\pi+\frac{2}{5}\pi=\frac{47}{5}\pi$$
More generally we have
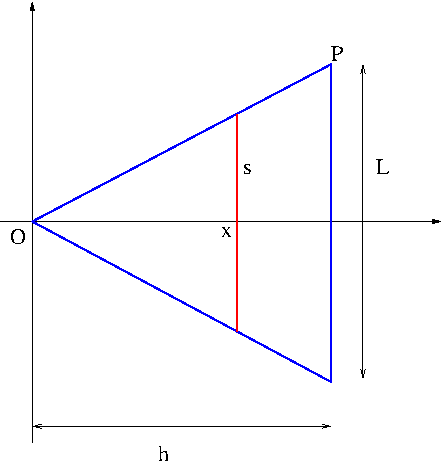
Cylindrical Shell Method
Suppose that the region under the curve $y=f(x)$, $a\leq x\leq b$ is revolved about the line $x=L$. Then the volume $V$ of the resulting solid is obtained by $$V=\left\{\begin{array}{ccc}\int_a^b 2\pi (x-L)f(x)dx & \mbox{if} & L\leq a\\\int_a^b 2\pi (L-x)f(x)dx & \mbox{if} & L\geq b\end{array}\right.$$
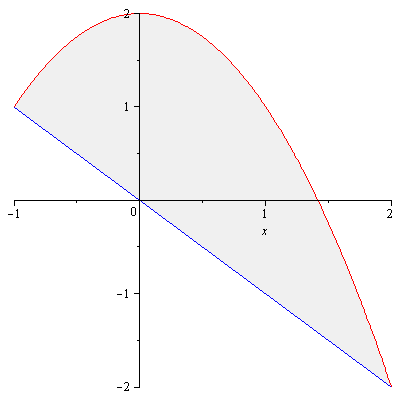
Example. The region enclosed by the $x$-axis and the parabola $y=3x-x^2$ is revolved about the vertical line $x=-1$. Find the volume of the resulting solid.
Solution. The region (in red) and the axis of rotation (in blue) are shown in Figure 5.
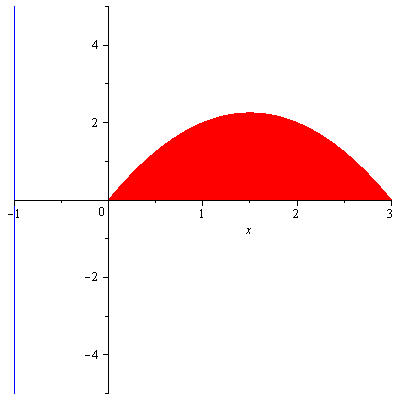
Figure 5
By cylindrical shell method, the volume $V$ is given by $$V=\int_0^3 2\pi(x+1)(3x-x^2)dx=\frac{45\pi}{2}$$
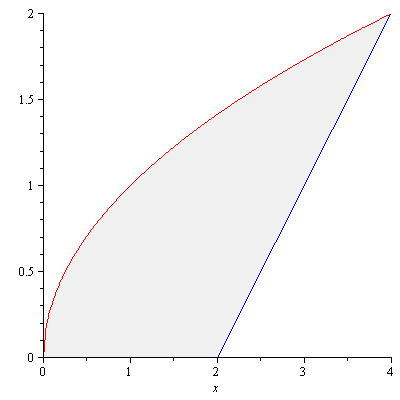
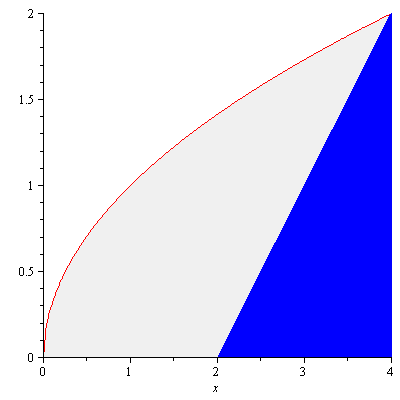
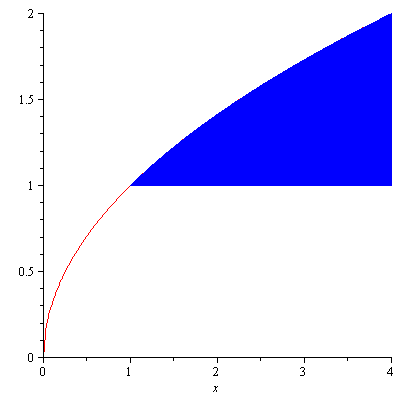
Example. The region bounded by the curve $y=\sqrt{x}$, the $x$-axis and the line $x=4$ is revolved about the $y$-axis. Find the volume of the resulting solid.
Solution. Figure 6 shows the region.
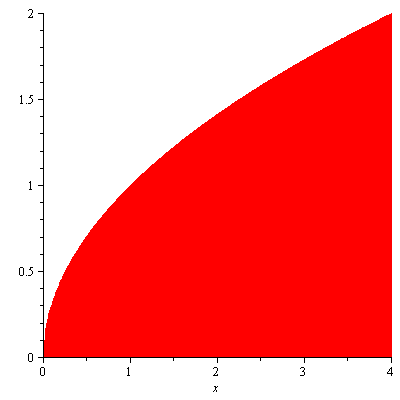
Figure 6
Since the axis of rotation is $x=0$, by cylindrical shell method the volume $V$ is given by $$V=\int_0^42\pi x\sqrt{x}dx=\frac{128\pi}{5}$$
Note that while cylindrical shell method is simpler, it is also easy to find the volume using washer method. $$V=\int_0^2\pi[4^2-(y^2)^2]dy=\int_0^2(16-y^4)dy=\frac{128\pi}{5}$$
Example. The same region in the previous example is revolved about the $x$-axis this time. Find the volume of the resulting solid using cylindrical shell method.
Solution. The solid and a cylindrical shell are shown in Figure 7.
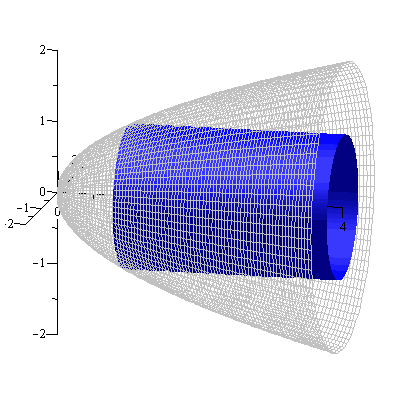
Figure 7
The shell radius is $y$ and the shell height $4-y^2$. Hence the volume is $$V=\int_0^2 2\pi y(4-y^2)dy=8\pi$$
Note that it would actually be easier to use disk method for this problem. Using disk method the volume $V$ is given by $$V=\int_0^4\pi(\sqrt{x})^2dx=\int_0^4\pi xdx=8\pi$$