$y=\sin x$ is not a one-to-one function so there cannot be an inverse function of $y=\sin x$. However we we restrict its domain to the closed interval $\left[-\frac{\pi}{2},\frac{\pi}{2}\right]$ it becomes a one-to-one function as shown in Figure 1.
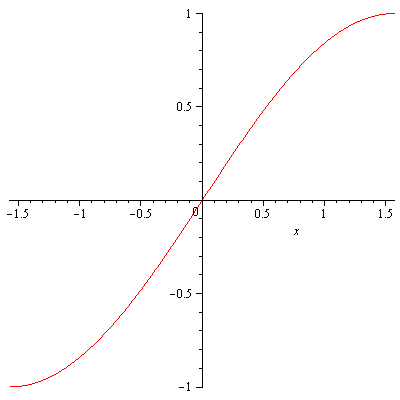
This means that we can consider $y=\sin^{-1}x$, the inverse function of $y=\sin x$. That is to say, $y=\sin^{-1}x$ is the value in $\left[-\frac{\pi}{2},\frac{\pi}{2}\right]$ for which $x=\sin y$. $y=\sin^{-1}x$ is also denoted by $y=\arcsin x$. Similarly,
- $y=\cos^{-1}x$ (or $y=\arccos x$) is the value in $[0,\pi]$ for which $x=\cos y$.
- $y=\tan^{-1}x$ (or $y=\arctan x$) is the value in $\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$ for which $x=\tan y$.
- $y=\cot^{-1}x$ (or $y=\mathrm{arccot} x$) is the value in $(0,\pi)$ for which $x=\cot y$.
Remark. In general, $y=\sin^{-1}x$ is an inverse relation of $y=\sin x$ which is multiple-valued. In order to consider differentiation, we require it to be single-valued and when $-\frac{\pi}{2}\leq\sin^{-1}x\leq\frac{\pi}{2}$ we call it the principal value of $\sin^{-1}x$ and denote it by $\mathrm{Sin}^{-1}x$. Throughout this note we will only consider principal values so we won’t be using the traditional notation like $y=\mathrm{Sin}^{-1}x$.
Recall that the graph of $y=f(x)$ and the graph of its inverse function $y=f^{-1}(x)$ are symmetric about the line $y=x$. Using this symmetry one can obtain the graph of an inverse trigonometric function. For example, Figure 2 shows the graph of $y=\sin x$ and the graph of $y=\sin^{-1} x$.
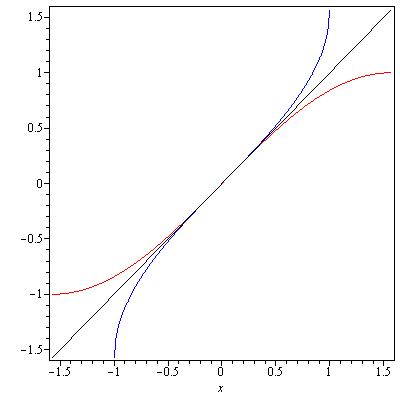
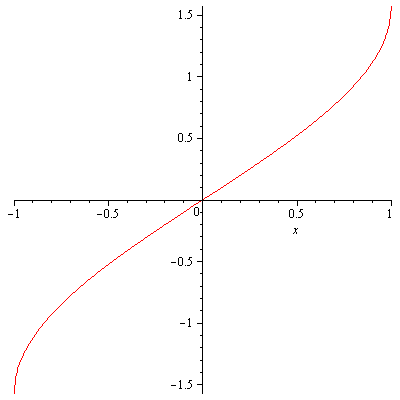
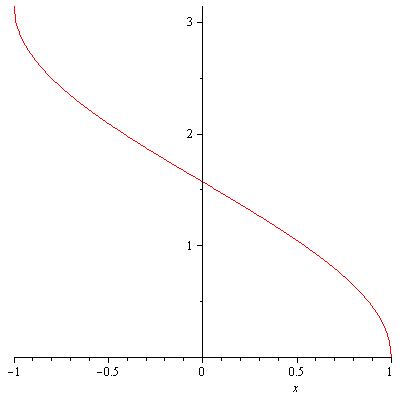

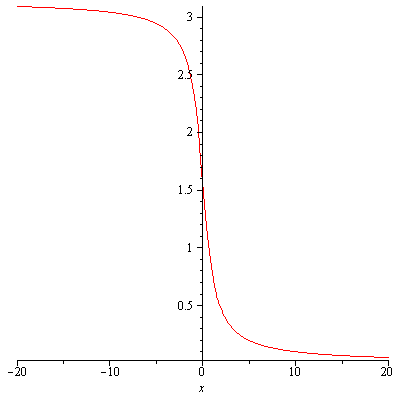
In addition, $y=\sec^{-1}x$ has domain $|x|\geq 1$ and range $\left[0,\frac{\pi}{2}\right)\cup\left(\frac{\pi}{2},\pi\right]$.
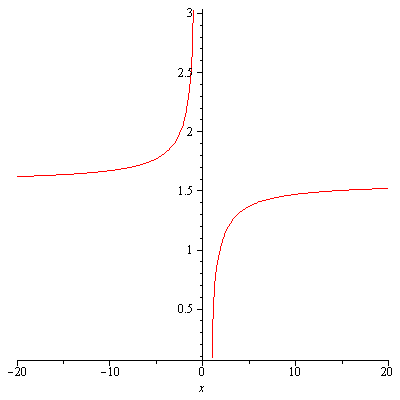
$y=\csc^{-1}x$ has domain $|x|\geq 1$ and range $\left[-\frac{\pi}{2},0\right)\cup\left(0,\frac{\pi}{2}\right]$.
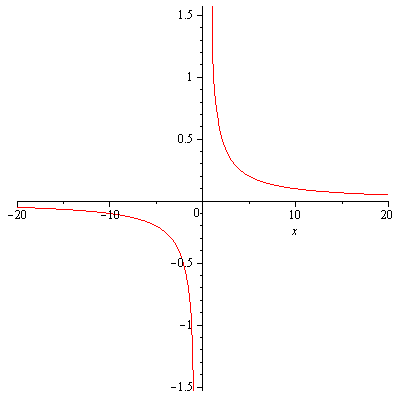
Inverse Functions and Their Derivatives
Let $y=f^{-1}(x)$ denote the inverse function of $f(x)$. Then \begin{equation}\label{eq:invfn}x=f(y)\end{equation} Differentiate \eqref{eq:invfn} with respect to $x$. \begin{equation}\label{eq:dinvfn}1=f'(y)\frac{dy}{dx}\end{equation} Solving \eqref{eq:dinvfn} for $\frac{dy}{dx}$ we have \begin{equation}\label{eq:dinvfn2}\frac{dy}{dx}=\frac{1}{f'(f^{-1}(x))}\end{equation}
Example. Let $f(x)=\ln x$. Knowing $f'(x)=\frac{1}{x}$ find the derivative of $f^{-1}(x)=e^x$.
Solution. Using \eqref{eq:dinvfn2} $$\frac{d}{dx}e^x=\frac{1}{\frac{1}{e^x}}=e^x$$
Although knowing the formula \eqref{eq:dinvfn2} is convenient, you can always find the derivative of an inverse function by following the same process of deriving \eqref{eq:dinvfn2}. It’s not actually anymore difficult or complicated than using \eqref{eq:dinvfn2}.
The Derivative of Inverse Trigonometric Functions
Let $f(x)=\sin x$. Then $f^{-1}(x)=\sin^{-1}x$. Using \eqref{eq:dinvfn2} \begin{align*}\frac{d}{dx}\sin^{-1}x&=\frac{1}{\cos(\sin^{-1}x)}\\&=\frac{1}{\sqrt{1-\sin^2(\sin^{-1}x)}}\\&=\frac{1}{\sqrt{1-x^2}}\end{align*} where $|x|<1$. The reason the sign in front of $\sqrt{}$ is positive is that $-\frac{\pi}{2}<\sin^{-1}x<\frac{\pi}{2}$ so $\cos(\sin^{-1}x)> 0$.
Alternative derivation: Let $y=\sin^{-1}x$. Then $x=\sin y$. By implicit differentiation $$1=\cos y\frac{dy}{dx}$$ Hence $$\frac{dy}{dx}=\frac{1}{\cos y}=\frac{1}{\cos(\sin^{-1}x)}=\frac{1}{\sqrt{1-x^2}}$$
If $u$ is a functions of $x$, then $$\frac{d}{dx}\sin^{-1}u=\frac{1}{\sqrt{1-u^2}}\frac{du}{dx},\ |u|<1$$ Similarly we obtain the rest of derivative formulas. \begin{align*}\frac{d}{dx}\cos^{-1}u&=-\frac{1}{\sqrt{1-u^2}}\frac{du}{dx},\ |u|<1\\\frac{d}{dx}\tan^{-1}x&=\frac{1}{1+u^2}\frac{du}{dx}\\\frac{d}{dx}\cot^{-1}x&=-\frac{1}{1+u^2}\frac{du}{dx}\\\frac{d}{dx}\sec^{-1}u&=\frac{1}{|u|\sqrt{u^2-1}}\frac{du}{dx},\ |u|>1\\\frac{d}{dx}\csc^{-1}x&=-\frac{1}{|u|\sqrt{u^2-1}}\frac{du}{dx},\ |u|>1\end{align*} In turns out we don’t really have to calculate all these formulas. We just need to calculate for example $\frac{d}{dx}\sin^{-1}x$, $\frac{d}{dx}\tan^{-1}x$, $\frac{d}{dx}\sec^{-1}x$ the rest can be obtained by inverse function-inverse cofunction identities \begin{align*}\cos^{-1}x&=\frac{\pi}{2}-\sin^{-1}x\\\cot^{-1}x&=\frac{\pi}{2}-\tan^{-1}x\\\csc^{-1}x&=\frac{\pi}{2}-\sec^{-1}x\end{align*}In case you haven’t seen this identities before they can be easily obtained from cofunction identities. For example sine and cosine are cofunctions of each other as you learned in trigonometry, namely $$\sin\left(\frac{\pi}{2}-x\right)=\cos x,\ \cos\left(\frac{\pi}{2}-x\right)=\sin x$$ Let $$\cos\left(\frac{\pi}{2}-y\right)=\sin y=x$$ Then $$\frac{\pi}{2}-y=\cos^{-1}x$$ i.e. the first identity above $$\cos^{-1}x=\frac{\pi}{2}-\sin^{-1}x$$
Integration Formulas
For any constant $a\ne 0$,
- $\int\frac{du}{\sqrt{a^2-u^2}}=\sin^{-1}\left(\frac{u}{a}\right)+C$, valid for $u^2<a^2$
- $\int\frac{du}{a^2+u^2}=\frac{1}{a}\tan^{-1}\left(\frac{u}{a}\right)+C$
- $\int\frac{du}{u\sqrt{u^2-a^2}}=\frac{1}{a}\sec^{-1}\left|\frac{u}{a}\right|+C$, valid for $|u|>a>0$
Example. \begin{align*}\int_{\sqrt{2}/2}^{\sqrt{3}/2}\frac{dx}{\sqrt{1-x^2}}&=\left.\sin^{-1}x\right|_{\sqrt{2}/2}^{\sqrt{3}/2}\\&=\sin^{-1}\left(\frac{\sqrt{3}}{2}\right)-\sin^{-1}\left(\frac{1}{\sqrt{2}}\right)\\&=\frac{\pi}{3}-\frac{\pi}{4}=\frac{\pi}{12}\end{align*}
Example. \begin{align*}\int\frac{dx}{\sqrt{3-4x^2}}&=\frac{1}{2}\int\frac{du}{\sqrt{3-u^2}} (u=2x)\\&=\frac{1}{2}\sin^{-1}\left(\frac{u}{\sqrt{3}}\right)+C\\&=\frac{1}{2}\sin^{-1}\left(\frac{2x}{\sqrt{3}}\right)+C\end{align*}
Example. \begin{align*}\int\frac{dx}{4x-x^2}&=\int\frac{dx}{4-(x-2)^2}\\&=\int\frac{du}{4-u^2} (u=x-2)\\&=\sin^{-1}\left(\frac{u}{2}\right)+C\\&=\sin^{-1}\left(\frac{x-2}{2}\right)+C\end{align*}
Example. \begin{align*}\int\frac{dx}{4x^2+4x+2}&=\int\frac{dx}{4\left(x+\frac{1}{2}\right)^2+1}\\&=\frac{1}{2}\int\frac{du}{u^2+1} (u=2x+1)\\&=\frac{1}{2}\tan^{-1}u+C\\&=\frac{1}{2}\tan^{-1}(2x+1)+C\end{align*}
Example. \begin{align*}\int\frac{dx}{e^{2x}-6}&=\int\frac{du}{u\sqrt{u^2-6}}\ (u=e^x)\\&=\frac{1}{\sqrt{6}}\sec^{-1}\left(\frac{e^x}{\sqrt{6}}\right)+C\end{align*} where $e^x>\sqrt{6}$ or equivalently $x>\ln\sqrt{6}\approx 0.8959$.
Integrating Inverses of Functions
Let $y=f^{-1}(x)$. Then $x=f(y)$ and $dx=f'(y)dy$. So with integration by parts, we have \begin{equation}\begin{aligned}\int f^{-1}(x)dx&=\int yf'(y)dy\\&=yf(y)-\int f(y)dy\\&=xf^{-1}(x)-\int f(y)dy\end{aligned}\label{eq:intinvfn}\end{equation} Using \eqref{eq:dinvfn2} we can also rewrite \eqref{eq:intinvfn} as \begin{equation}\label{eq:intinvfn2}\int f^{-1}(x)dx=xf^{-1}(x)-\int\frac{x}{f'(f^{-1}(x))}dx\end{equation}
Using \eqref{eq:intinvfn}\begin{align*}\int\cos^{-1}xdx&=x\cos^{-1}x-\sin y+C\\&=x\cos^{-1}x-\sin(\cos^{-1}x)+C\end{align*}Since $x=\cos y$, $$\sin(\cos^{-1}x)=\sin y=\sqrt{1-x^2}$$ (Recall that $0\leq\cos^{-1}x\leq\pi$ so $\sin^{-1}x\geq 0$.) Hence, \begin{equation}\label{eq:intinvcos}\int\cos^{-1}xdx=x\cos^{-1}x-\sqrt{1-x^2}+C\end{equation} Of course one can obtain \eqref{eq:intinvcos} using \eqref{eq:intinvfn2} though the required calculation is a bit longer. The integral \eqref{eq:intinvcos} can be also found without using \eqref{eq:intinvfn} or \eqref{eq:intinvfn2}. Using integration by parts\begin{align*}\int\cos^{-1}xdx&=x\cos^{-1}x+\int\frac{x}{\sqrt{1-x^2}}dx\\&=x\cos^{-1}x-\sqrt{1-x^2}+C\end{align*} The rest of the integrals of inverse trigonometric functions are given by\begin{align*}\int\sin^{-1}xdx&=x\sin^{-1}x+\sqrt{1-x^2}+C\\\int\tan^{-1}xdx&=x\tan^{-1}x-\frac{1}{2}\ln(1+x^2)+C\\\int\cot^{-1}xdx&=x\cot^{-1}x+\frac{1}{2}\ln(1+x^2)+C\\\int\sec^{-1}xdx&=x\sec^{-1}x-\frac{x}{|x|}\ln|x+\sqrt{x^2-1}|+C\\\int\csc^{-1}xdx&=x\csc^{-1}x+\frac{x}{|x|}\ln|x+\sqrt{x^2-1}|+C\end{align*}
