Consider a solid each of which parallel cross sections has its area represented by the function $A(x)$, $a\leq x\leq b$. The volume element is then given by $dV=A(x)dx$. Hence the volume of the solid is obtained by the integral \begin{equation}\label{eq:volslice}V=\int_{x=a}^{x=b}dV=\int_a^b A(x)dx\end{equation}

Example. Find the volume of a pyramid whose base is a square with side $L$ and whose height is $h$.

Solution. See Figure 1.

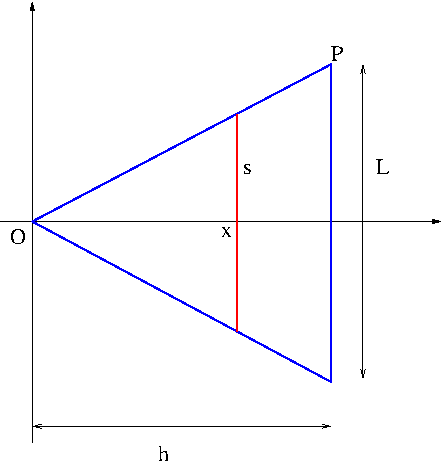
Figure 1

We find the ratio $x$ to $h$ $\frac{x}{h}=\frac{\frac{s}{2}}{{\frac{L}{2}}}=\frac{s}{L}$. So we have $s=\frac{L}{h}x$. (Another observation is the line segment $\overline{OP}$ has slope $\frac{\frac{L}{2}}{h}=\frac{L}{2h}$ so the equation of line through $\overline{OP}$ is $y=\frac{L}{2h}x$ and for $y=\frac{s}{2}$ we get $s=\frac{L}{h}x$.) The area $A(x)$ of the cross section at $x$ is $A(x)=s^2=\frac{L^2}{h^2}x^2$. Hence $$V=\int_0^h A(x)dx=\frac{L^2}{h^2}\int_0^h x^2dx=\frac{1}{3}L^2h$$

Example. Show that the volume of a right circular cone whose circular base has radius $r$ and whose height is $h$ is $V=\frac{1}{3}\pi r^2h$.

Solution. Left as an exercise.

Example. Show that the volume of a sphere of radius $r$ is $V=\frac{4}{3}\pi r^3$.

Solution. See Figure 2.

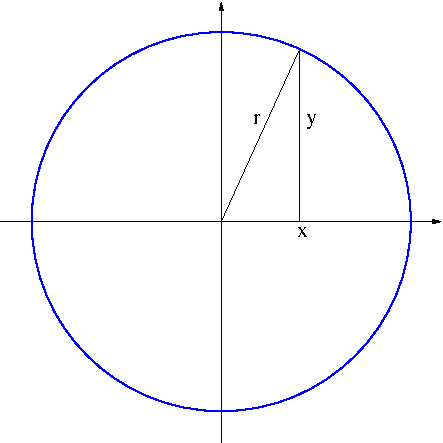
Figure 2

$y=\sqrt{r^2-x^2}$ so $A(x)=\pi y^2=\pi (r^2-x^2)$. Hence the volume $V$ is \begin{align*}V&=\int_{-r}^r A(x)dx\\&=\int_{-r}^r \pi (r^2-x^2)dx\\&=2\pi\int_0^r (r^2-x^2)dx\\&=2\pi\left[r^2x-\frac{x^3}{3}\right]_0^r\\&=\frac{4}{3}\end{align*}

Example. Consider a solid with a circular base of radius 1 whose parallel cross secxtions perpendicular to the base are equilateral triangles. Find the volume of the solid.

Solution. See Figure 3.

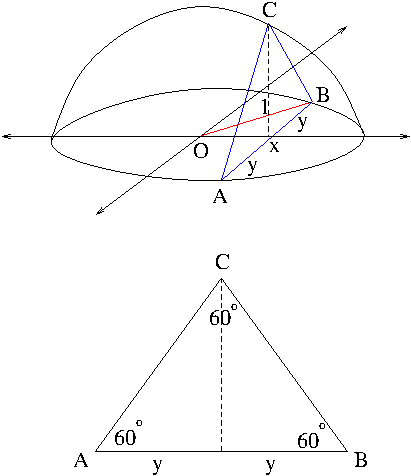
Figure 3

From the picture we see that $$A(x)=\frac{1}{2}(2y)(\sqrt{3}y)=\sqrt{3}y^2=\sqrt{3}(1-x^2)$$ Hence the volume $V$ is given by $$V=\int_{-1}^1 A(x)dx=\sqrt{3}\int_{-1}^1(1-x^2)dx=2\sqrt{3}\int_0^1(1-x^2)dx=\frac{4\sqrt{3}}{3}$$

Example. A Curved wedge is cut from a cylinder of radius 3 by two planes. One plane is perpendicular to the axis of the cylinder. The other plane is crossing the first plane at a $45^\circ$ angle at the center of the cylinder.

Solution. See Figure 4.

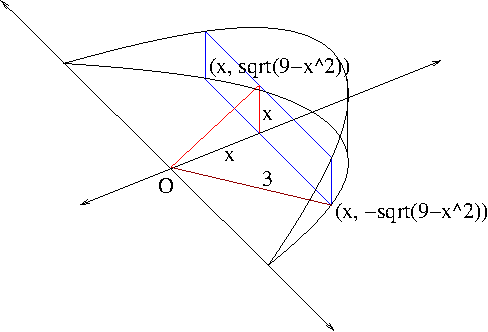
Figure 4

The cross section at $x$ is the rectangle in blue. It’s area is $$A(x)=\mbox{length}\times\mbox{width}=2\sqrt{9-x^2}\times x=2x\sqrt{9-x^2}$$ Hence the volume $V$ is given by \begin{align*}V&=\int_0^3 2x\sqrt{9-x^2}dx\\&=-\int_9^0\sqrt{u}du\ (u=9-x^2)\\&=\int_0^9\sqrt{u}du\\&=\frac{2}{3}[u^{\frac{3}{2}}]_0^9\\&=18\end{align*}