Back when I was a Ph.D. student, a friend of mine (he was a Ph.D. student in physics studying laser optics) asked me if the series $\sum_{n=0}^\infty e^{nix}$ converges. I vaguely remember that his advisor needed to have a finite value for the infinite sum for whatever reason I don’t remember. At that time, I didn’t know other summability methods and I only knew the conventional definition of infinite sums. The series is a geometric series with $r=e^{ix}$ and since $|e^{ix}|=1$, I bluntly told him that you can’t have a finite value for the series. It diverges!
I don’t know what motivated me but I just thought about the series $\sum_{n=0}^\infty e^{nix}$ and I was wondering if it is Cesàro summable. I was able to show that indeed it is. To my pleasant surprise, the Cesàro sum of $\sum_{n=0}^\infty e^{nix}$ is $\frac{1}{1-e^{ix}}$. I am sure that this is well-known and I am just being ignorant about it. I would appreciate if someone can tell me any reference where the Cesàro sum of $\sum_{n=0}^\infty e^{nix}$ appears.
The $(n+1)$-th partial sum $S_{n+1}$ of $\sum_{n=0}^\infty e^{nix}$ is
\begin{align*}
S_{n+1}&=\sum_{k=0}^n e^{nix}\\
&=1+e^{ix}+e^{2ix}+\cdots+e^{nix}\\
&=\frac{1-e^{(n+1)ix}}{1-e^{ix}}
\end{align*}
provided $x\ne 2m\pi$, $m\in\mathbb{Z}$. Now the sum of the first $n$ partial sums is calculated to be
$$\sum_{k=0}^{n-1}S_k=\frac{1}{1-e^{ix}}\left[(n+1)-\frac{1-e^{(n+1)ix}}{1-e^{ix}}\right].$$
The Cesàro sum of $\sum_{n=0}^\infty e^{nix}$ is
\begin{align*}
\sum_{n=0}^\infty e^{nix}&=\lim_{n\to\infty}\frac{\sum_{k=0}^{n-1}S_k}{n}\\
&=\frac{1}{1-e^{ix}}
\end{align*}
as $\lim_{n\to\infty}\frac{1}{n}\frac{1-e^{(n+1)ix}}{1-e^{ix}}=0$. For $x=2m\pi$ with $m\in\mathbb{Z}$, $\sum_{n=0}^\infty e^{nix}=1+1+1+\cdots$ is not Cesàro summable as its Cesàro sum is \begin{align*}
1+1+1+\cdots&=\lim_{n\to\infty}\frac{\sum_{k=1}^n S_k}{n}\\
&=\lim_{n\to\infty}\frac{\frac{n(n+1)}{2}}{n}\\
&=\infty.
\end{align*}
However, it can be shown that $1+1+1+\cdots=-\frac{1}{2}$ using zeta function regularization. (I also discussed it here.)
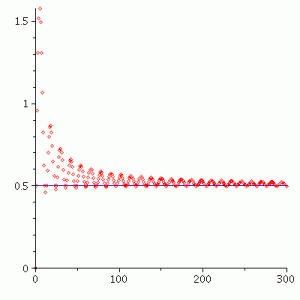
This figure shows the real part of the Cesàro sum $\sum_{n=0}^\infty e^{nix}$ with $x=\frac{\pi}{6}$ converging to the real part of $\frac{1}{1-e^{ix}}=\frac{1}{2}$.
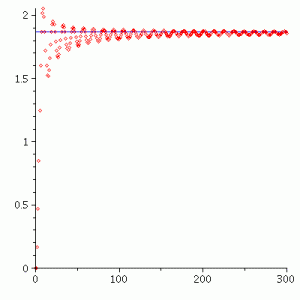
This figure shows the imaginary part of the Cesàro sum $\sum_{n=0}^\infty e^{nix}$ with $x=\frac{\pi}{6}$ converging to the imaginary part of $\frac{1}{1-e^{ix}}=\frac{\sin x}{2(1-\cos x)}$.
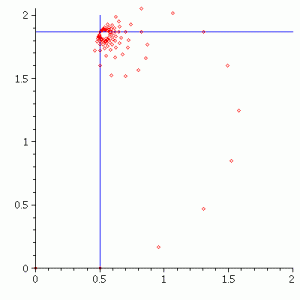
Finally this figure shows the Cesàro sum $\sum_{n=0}^\infty e^{nix}$ with $x=\frac{\pi}{6}$ converging to $\frac{1}{1-e^{ix}}$.

Hi Sung. I have two comments.
1. Here is how Feynman handles your series:
F(a)=\sum_n=0 (a \exp{ix)^n where $a$ is a real number less than unity.
F(a)= 1/(1-a exp{ix} is now quite rigorous. Since the original series was
divergent, it is unclear what it is “trying” to represent; so this is one way (which
actually occurs in physics) to regularized the series. Now just set a=1. 🙂
I was not aware of the Cesaro summability, but I do recall seeing that idea.
Wish I could remember where.
2. I was intrigued by your comment on renormalization in this thread. People seem to
think that this is necessary because the (field) theory diverges – not so;
Renormalization would still be necessary even if the theory were finite! For example,
suppose one wishes to calculate physical quantities like P1(m) and P2(m), where
m is a physical parameter (mass or charge for instance). Of course there may be
infinitely many such quantities, but let’s say just two as an example. Now, it is
unknown what the parameter ‘m’ is a-priori – it is just a “bare” parameter in the theory
(an unknown number in a Lagrangian). How can one get this value? You can only
measure real physical quantities, not unknown parameters. So, in the expressions for,
say, P1(m) insert a cutoff, L, on the integral (which is over all values of momentum
perhaps) which defines P1 -> P1(m,L). Note I have not said whether or not the
defining integral converges or diverges; it could be either (and that is the point).
Now, P2(m,L) which I want to predict, contains L also. Now invert the expression
for P1: m=f(P1,L). Next, substitute this into P2 -> P2(f(P1,L),L). Ok, we have
now two parameters in P2: L and P1. Now go into the lab and *measure* P1, substituting
the result into this last expression. Finally remove the cutoff: thus, the *prediction*
for P2 (or any other P as well using the same procedure and same m=f(P1,L) ), is
P2 = lim_{L \to \infty} P2(f(P1_exp,m),m).
This procedure must be done *regardless* of whether or not the original integral(s)
were finite or infinite; that is because the “bare” paramenter(s) (here, just m) must
somehow be replaced by experimental numbers, and the parameter(s) m are not
directly measurable. The miracle is that even *if* the integrals for P1, P2, …, are
infinite, the renormalized quantities are indeed *finite* (and can be proved to
be finite in certain theories, such as gauge theories).
LRM
Hi Larry,
The Feynman’s idea you mentioned is, while it appears to be brilliant, not mathematically correct. It is correct that $\sum_{n=0}^\infty \epsilon e^{nix}=\frac{1}{1-\epsilon e^{ix}}$ provided $|\epsilon|<1$. While $\lim_{\epsilon\to 1}\frac{1}{1-\epsilon e^{ix}}=\frac{1}{1-e^{ix}}$,
$$\lim_{\epsilon\to 1}\sum_{n=0}^\infty \epsilon e^{nix}\ne\sum_{n=0}^\infty e^{nix}$$ since the LHS is finite but the RHS is not. The limit and the infinite sum would've been exchangeable if $\sum_{n=0}^\infty e^{nix}$ were finite. So, the Feynman's idea would not actually prove that $\sum_{n=0}^\infty e^{nix}=\frac{1}{1-e^{ix}}$ and this can't be true as long as we use the conventional notion of infinite sum.
It is shame to admit for a professional mathematician, but I was not aware of other summability methods until last year. One day last year I visited Khin and Floyd was there with Khin. Floyd was excited to tell me that $1+2+3+\cdots=-\frac{1}{12}$ and I, knowing only the conventional infinite sum, said it's nonsense. Later I realized that there is much more to the infinite sum than meets the eye. I learned about other summability methods including Cesaro summation, Abel summation, Borel summation, and zeta function regularization. But more importantly I realized that I actually didn't truly know what the infinite sum $\sum_{n=0}^\infty a_n$ means (and no one does). The one notion (the conventional one) I knew was merely one possibility. I also realized that if one does not accept the conventional notion of infinite sum, there is no reason $1+2+3+\cdots$ should be infinity and that all known laws of arithmetic do not necessarily hold for infinite sums including the Archemedes' principle that "the whole is greater than its part." Interestingly, the notion of an alternative summability method that could give rise to a finite value for a divergent series did not sit well with mainstream mathematicians when it was introduced for the first time. When Srinivasa Ramanujan showed his proof of $1+2+3+\cdots=-\frac{1}{12}$ to his mentor and collaborator G. H. Hardy, Hardy did not take it seriously. Also when Emile Borel showed Mittag-Leffler his summation method that could give a finite answer for a divergent series, Mittag-Leffler said (in Latin) "The Master forbids it." Maybe the conventional notion of infinite sum is not the correct one. I am now also thinking that the divergence issue arising in physics may be resolved once we understand the correct notion of infinite sum.
Well, it is my understanding that (at least some) divergent series are asymptotic.
For example, the series 1-1! x + 2! x^2 +3! x^3 … is an asymptotic series for
the Borel function (Borel sum, therefore)
\int dt \exp (-t) / (1+xt) . While the limit of an asymptotic series does not exist,
\lim x -> x0 f(x)/ \sum^n (x) approaches unity; that is, instead of convergence
as the number of terms goes to infinity, there is convergence of an (optimal) fixed
number of terms as the variable approaches the asymptote. It has been conjectured
that the perturbation series for QED (a renormalizable theory) is indeed asymptotic
as p-> 0 (momentum) and that all that renormalization is doing is to find the function
to which the series (in p) is asymptotic, similar to the Borel sum above. There is an
explicit example in Carl Bender’s thesis where it is rigorously shown that the perturbation series (in g) of the ground state eigenvalue of H = 1/2 p^2 +1/2 x^2+ g x^4 *is* an asymptotic series (as; no one knows to what) as g -> 0.
Regarding Feynmans trick, it is just one way to regularize the series; other methods
may give other results. BTW, it is now common practice to regularize using the
dimension of space: “dimensional regularization”. One writes D = 4-e, expands
in powers of e (small) then takes the limit as e ->0 at the end of the calculation.
This allows one to regularize QED for example without momentum cutoffs. Why is
this better? Cutting off the integrals destroys gauge invariance (even more important
than Lorentz invariance) whereas dimensional regularization does not. 🙂
That asymptotic series should have read:
$1-1! x + 2! x^2 – 3! x^3 +- … $ alternating in sign.
LRM
Pingback: Infinite Series | MathPhys Archive