Problem: Given $x,y\geq 0$ satisfying \begin{equation}\label{eq:ellipse}x+y+\sqrt{2x^2+2xy+3y^2}=4\end{equation} prove $x^2y<4$. (Hat tip: Sam Walters)

Solution. First rewrite \eqref{eq:ellipse} as \begin{equation}\label{eq:ellipse2}\sqrt{2x^2+2xy+3y^2}=4-x-y\end{equation} Squaring \eqref{eq:ellipse} we obtain an equation of ellipse \begin{equation}\label{eq:ellipse3}(x+4)^2+2(y+2)^2=40\end{equation} (Figire 1)

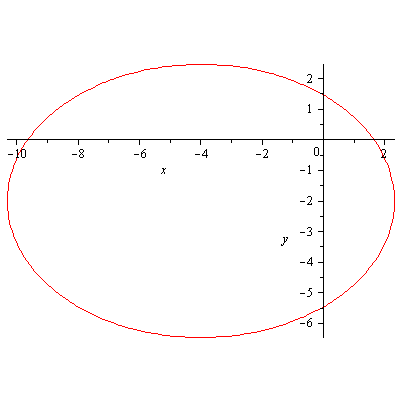
Figure 1

Graphically we see that the inequality holds as shown in Figure 2.

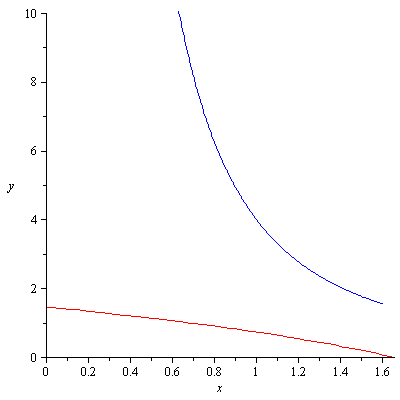
Figure 2. Ellipse (x+4)^2+2(y+2)^2=40, x=0..-4+sqrt(40) (red) and y=4/x^2 (blue)

Suppose $x>0$ (for $x=0$ the inequality $x^2y<4$ is trivial). Since $x>0,y>0$ then, $$x^2y<4\Longleftrightarrow (y+2)^2<\left(\frac{4}{x^2}+2\right)^2$$ Solve \eqref{eq:ellipse3} for $(y+2)^2$. \begin{equation}\label{eq:ellipse4}(y+2)^2=20-\frac{(x+4)^2}{2}\end{equation} Now subtract $\left(\frac{4}{x^2}+2\right)^2$ from the RHS of \eqref{eq:ellipse4}. $$20-\frac{(x+4)^2}{2}-\left(\frac{4}{x^2}+2\right)^2=\frac{-x^6-8x^5+16x^4-32x^2-32}{2x^4}<0$$ since $-x^6-8x^5+16x^4-32x^2-32<0$ for $0<x<-4+\sqrt{40}$ as shown in Figure 3.

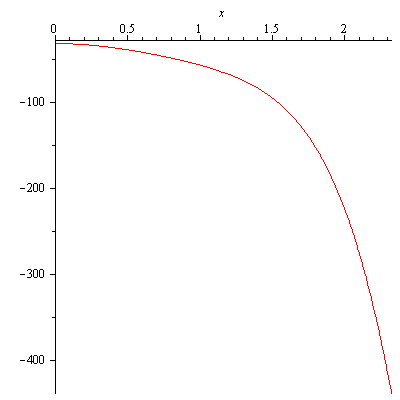
Figure 3. The graph of f(x)=-x^6-8x^5+16x^4-32x^2-32, x=0..-4+sqrt(40)

Update: Republic of Math graphically came up with a sharper inequality $x^2y<1$. The graphics can be seen here. As you can see in the graphics, there is still room for even (slightly) more sharp inequality. In fact $x^2y<0.9$ as you can see in Figure 4 below.

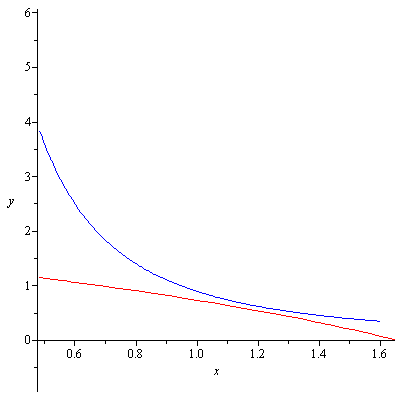
Figure 4. Ellipse (x+4)^2+2(y+2)^2=40, x=0..-4+sqrt(40) (red) and y=0.9/x^2 (blue)

Update: While I could not analytically find the smallest value of $a>0$ such that $x^2y<a$, I found graphically that $a$ can be as small as $0.789$. Figure 5 and Figure 6 are the graphs of $f(x)=-x^6-8x^5+16x^4-8ax^2-2a^2$ for $0\leq x\leq -4+\sqrt{40}$ for $a=0.789$ and for $a=0.788$, respectively. For $a=0.789$, $f(x)<0$ on $[0,-4+\sqrt{40}]$.

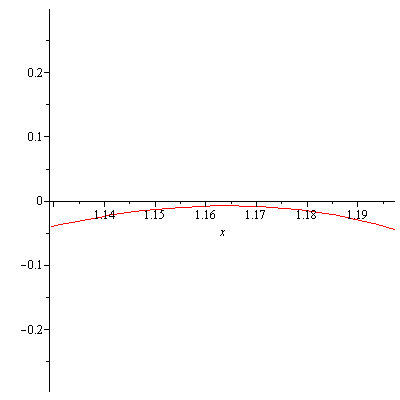
Figure 5. The graph of f(x)=-x^6-8x^5+16x^4-8ax^2-2a^2 (for a=0.789), x=0..-4+sqrt(40)

But with $a=0.788$ $f(x)$ is no longer negative for all $x$ in $[0,-4+\sqrt{40}]$.

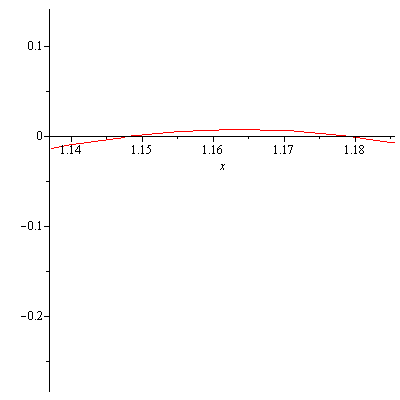
Figure 5. The graph of f(x)=-x^6-8x^5+16x^4-8ax^2-2a^2 (for a=0.788), x=0..-4+sqrt(40)