The derivative of the volume $V=\frac{4}{3}\pi r^3$ of a sphere of radius $r$ with respect to $r$ is the surface area $S=4\pi r^2$. Is this a coincidence? It is not. There is a good reason why it happened that way. To understand it more easily, let us take a look at it’s lower dimensional analogue, namely the derivative of the area $\pi r^2$ of a circle of radius $r$ is the circumference $2\pi r$. Let me first explain why we get that. Let $A(r)=\pi r^2$. Then
$$\frac{dA}{dr}=\lim_{\Delta r\to 0}\frac{\pi(r+\Delta r)^2-\pi r^2}{\Delta r}.$$
$\pi(r+\Delta r)^2-\pi r^2$ is the area (shape of washer) between two circles both centered at the origin with radii $r+\Delta r$ and $r$, respectively as seen in the following figure:
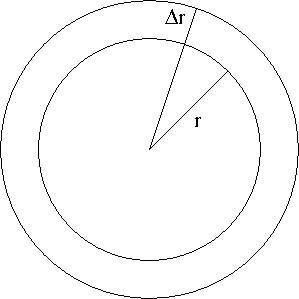
As $\Delta r$ gets smaller, you see that the washer gets thiner. So if $\Delta r\to 0$, the washer becomes circle of radius $r$ resulting $\frac{dA}{dr}$ its circumference. By doing the same analysis, you can see why the derivative of the volume of sphere is its surface area.
Do any other objects share the relationship? Sure! For instance, the derivative of the area $x^2$ of a square with side $x$ is its circumference $2x$. The derivative of the volume $\pi r^2h$ of a cylinder with radius $r$ and height $h$ is its lateral surface area $2\pi rh$. How about a cube with volume $V=x^3$? In this case the derivative is $3x^2$ so it is not the surface area. Why is this? It is due to symmetry i.e. it depends on whether the volume increases symmetrically when you increase your variable such as length of side, radius, or height, etc. In case of a cube, increasing length from $x$ to $x+\Delta x$ results in the increase of volume from only three faces of the cube i.e. the volume of cube does not increase symmetrically in that case. When $\Delta x\to 0$, the volume increment becomes three faces resulting the derivative the area of those three faces $3x^2$.
How about a box with volume $V=xyz$? In this case, divergence would give a similar relationship. In fact, $\nabla\cdot V=\frac{\partial V}{\partial x}+\frac{\partial V}{\partial y}+\frac{\partial V}{\partial z}=yz+xz+xy$ which is the surface area of box with length $x$, width $y$ and height $z$. Imagine that a box is filled with fluid and assume that volume increase amounts to the fluid flowing into the box through its faces. $\frac{\partial V}{\partial x}$ would measure the rate of fluid flowing into the $yz$ face per unit time. That would indeed be the same as the area of the face $yz$.

It does work if you calculate the dimensions of the square with respect to the distance from the centre of the square to the middle of one of its sides.
For example: Let S=side of the square, and let s = S/2 (the distance from the centre to the middle of a side is half the side).
Area = (2s)^2 = 4s^2
Perimeter = 8s
The derivative of 4s^2= 8s
Therefore the derivative for the area of a square is the perimeter of a square when the formula is expressed in terms of the distance from the centre of the square to the middle of its side.
It works for cubes with volume and surface area too (just as for spheres and their surface area).
Volume = (2s)^3 = 8s^3
Surface area = 6(2s)^2 = 6x4s^2 = 24s^2
Derivative of 8s^2 = 24s^2
In fact, it works for any figure with equal sides. You just need to rewrite the commonly used formula (often written in terms of a side) to be expressed in terms of the centre to the midpoint of an edge (2 dimensional) or the centre to the middle of a face (3 dimensional).
Remember, radius isn’t a side of a circle, it’s the dimension representing the distance from the centre to the edge. If you express any other shape with equal sides in the same terms (distance from the centre to the nearest edge), you’ll be expressing that formula in the same terms that we normally use for things that include circles. Then you’ll find that the derivative method will allow you to determine the formula for surface area from the formula for volume, and the formula for perimeter from the formula for area.
If you find my explanation skips over some of the fancy math, you can get a more detailed explanation at the link here:
https://apcentral.collegeboard.org/courses/resources/do-cubes-squares-have-same-properties-spheres-circles
Can someone please explain, in the simplest of terms, why in the case of a Sphere one can differentiate its volume to find its surface area, but when one attempts this with the volume of a Cube it doesn’t work? Thanks, Mick.
Have you read the article? I answered all your questions there.
It does work if you calculate the dimensions of the square with respect to the distance from the centre of the square to the middle of one of its sides.
For example: Let S=side of the square, and let s = S/2 (the distance from the centre to the middle of a side is half the side).
Area = (2s)^2 = 4s^2
Perimeter = 8s
The derivative of 4s^2= 8s
Therefore the derivative for the area of a square is the perimeter of a square when the formula is expressed in terms of the distance from the centre of the square to the middle of its side.
It works for cubes with volume and surface area too (just as for spheres and their surface area).
Volume = (2s)^3 = 8s^3
Surface area = 6(2s)^2 = 6x4s^2 = 24s^2
Derivative of 8s^2 = 24s^2
In fact, it works for any figure with equal sides. You just need to rewrite the commonly used formula (often written in terms of a side) to be expressed in terms of the centre to the midpoint of an edge (2 dimensional) or the centre to the middle of a face (3 dimensional).
Remember, radius isn’t a side of a circle, it’s the dimension representing the distance from the centre to the edge. If you express any other shape with equal sides in the same terms (distance from the centre to the nearest edge), you’ll be expressing that formula in the same terms that we normally use for things that include circles. Then you’ll find that the derivative method will allow you to determine the formula for surface area from the formula for volume, and the formula for perimeter from the formula for area.
If you find my explanation skips over some of the fancy math, you can get a more detailed explanation at the link here:
https://apcentral.collegeboard.org/courses/resources/do-cubes-squares-have-same-properties-spheres-circles
That’s again due to symmetry. If you use $s=\frac{x}{2}$ instead of the side $x$, the area of the square increases symmetrically when $s$ increases. Increasing from $s$ to $s+\Delta s$ results in the increase of area from all four sides of the square.
“The derivative of the area x2 of a square with side x is its circumference 2x”. But this is wrong. The circumference of a square should be 4x.
Adam,
Thanks! You are right. The derivative of the area $x^2$ of a square does not coincide with its circumference $4x$ for the same reason why the derivative of the volume $x^3$ of a cube does not coincide with its surface area $6x^2$.
The surface area of a cube is not 4x^2, it is 6x^2 (a die has 6 sides).
It *does* work if you calculate using the distance from the centre to the middle of a face instead of the lengths of one of the sides.
Yes of course. It is $6x^2$. Thanks for the correction.
cool articel thanks 🙂 i like it!